넘치게 채우기
[선형대수] 1-2. 선형방정식의 소거 본문
선형시스템의 해를 구하는 한 방법은 소거법(method of elimination)이다.
소거법은 원래의 시스템과 동치인 해를 더 쉽게 구할 수 있는 식으로 변형하는 것이다.
⭐️선형시스템에서는 3가지의 행 연산으로 원래의 식과 동치인 선형방정식으로 변환할 수 있다.
- 한 방정식에 0이 아닌 상수를 곱하기
- 방정식들의 위치를 서로 교환
- 한 방정식에 0이 아닌 상수를 곱하여 다른 방정식에 더하기
선형시스템의 3가지 해의 경우를 보면서 해를 구해보도록 하자.
1. 해가 하나인 경우
x1 - 3x2 = -3
2x1 + x2 = 8
첫 번째 식에 -2를 곱하여 두 번째 식에 더하여 x1이 없는 방정식을 구할 수 있다.
x2 = 2가 나오고, 첫 번째 식에 대입하면 x1 = 3이란 해를 얻을 수 있다.
이는 유일한 해가 된다.
두 직선은 한 점에서 만난다.

2. 해가 없는 경우
x1 - 2x2 = 4
2x1 - 4x2 = 4
첫 번째 식에 -2를 곱하여 두 번째 식에 더하면 0=-4라는 모순된 식이 나온다.
이런 경우에는 해를 가지지 않는다.
기하학적으로는 두 직선이 평행하여 만나지 않음을 의미한다.
3. 해가 무한한 경우
x1 - 2x2 = 8
2x1 - 4x2 = 16
첫 번째 식에 -2를 곱하여 두 번째 식에 더하면 x1 - 2x2 = 8과 0=0이 남는다.
이 경우에는 기하학적으로 두 직선이 일치하는 것을 의미한다.
가우스 소거법
가우스에 의해 변수들을 체계적으로 소거하는 효율적인 방법이 체계화되었다.
이를 가우스 소거법(Gaussian elimination)이라고 한다.
⭐️아래의 3가지 연산을 반복적으로 적용하면 된다.
- 한 방정식에 0이 아닌 상수를 곱한다.
- 방정식들의 위치를 서로 교환한다.
- 한 방정식에 0이 아닌 상수를 곱하여 다른 방정식에 더한다.
가우스-조단 소거법
- 전향 소거법: 각 방정식에다 다른 식의 변수의 계수와 반대가 되도록 적절한 상수를 곱하여 두 식을 더하여 해당하는 변수들을 차례로 소거한 새로운 방정식 L을 구한다.
- 역대입법: 새로운 방정식 L로부터 하나의 변수 값을 구한 후 남은 식들에 차례로 대입하여 전체 해를 구한다.
이 두가지 과정을 합하여 가우스-조단(Gauss-Jordan elimination)이라고 하며, 1단계인 전향 소거법을 가우스 소거법이라고 한다.
가우스 소거법 과정에서 각 식의 가장 앞에 있는 0이 아닌 계수를 피벗(pivot)으로 정할 수 있다.
피벗을 중심으로 소거하는 것이 효율적이고, 피벗이 단순한 수(1, 2 등)일수록 계산이 편리하다.
연습: 가우스 조단 소거법으로 해를 구해보기
x - 3y - 2z = 6
2x - 4y - 3z = 8
-3x + 6y + 8z = -5
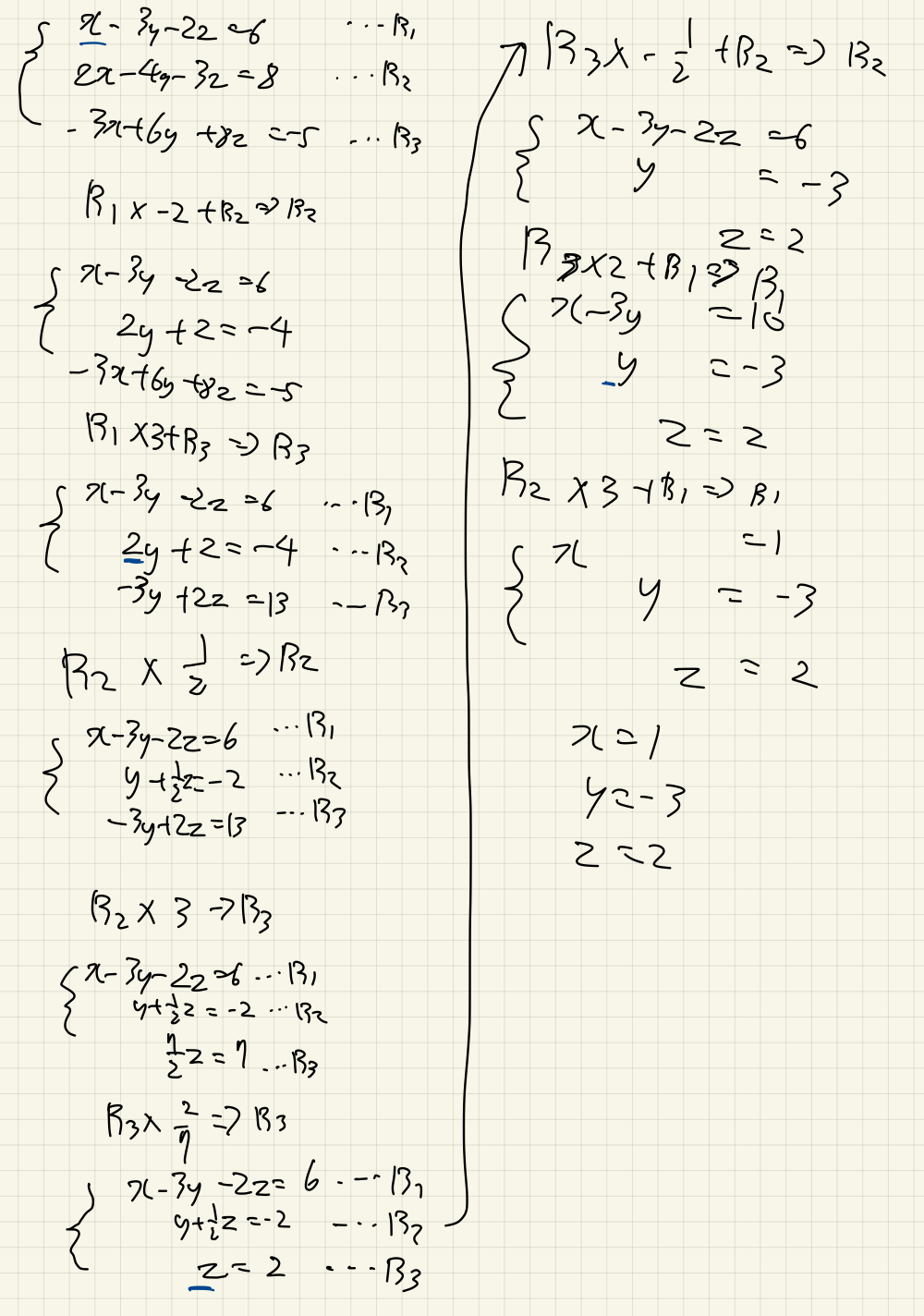
'수학 > 선형대수' 카테고리의 다른 글
| [선형대수] 3-2. 역행렬과 선형시스템의 해 (0) | 2024.01.06 |
|---|---|
| [선형대수] 3-1. 행렬식과 여인수 (0) | 2024.01.05 |
| [선형대수] 2-2. 특수한 행렬과 기본 행 연산 (0) | 2024.01.04 |
| [선형대수] 2-1. 행렬, 행렬의 연산 (0) | 2024.01.03 |
| [선형대수] 1-1. 선형대수와 선형시스템 (0) | 2024.01.01 |




