넘치게 채우기
[선형대수] 3-1. 행렬식과 여인수 본문
행렬식
행렬식(Determinant)이란 정방행렬 A에서 하나의 스칼라 값을 대응시키는 함수로써, Det(A) 또는 |A|로 표시한다.
n차 정방행렬의 행렬식을 n차 행렬식이라고도 부른다.
즉, A를 n x n행렬이라고 할 때 행렬 A에 대해 A의 행렬식이라는 수가 대응된다.
기호로는 행렬 A의 괄호 대신 수직 막대선을 그어서 나타낸다.

행렬식을 구하는 두 가지 방법
사루스의 공식
주 대각선 방향으로 원소들을 곱한 값을을 더한 값에
주 대각선 반대 방향으로 원소들을 곱한 값들의 덧셈의 역원을 더한다고 생각하면 편리하다.
아래는 2*2의 크기와 3*3의 크기의 예시이다.

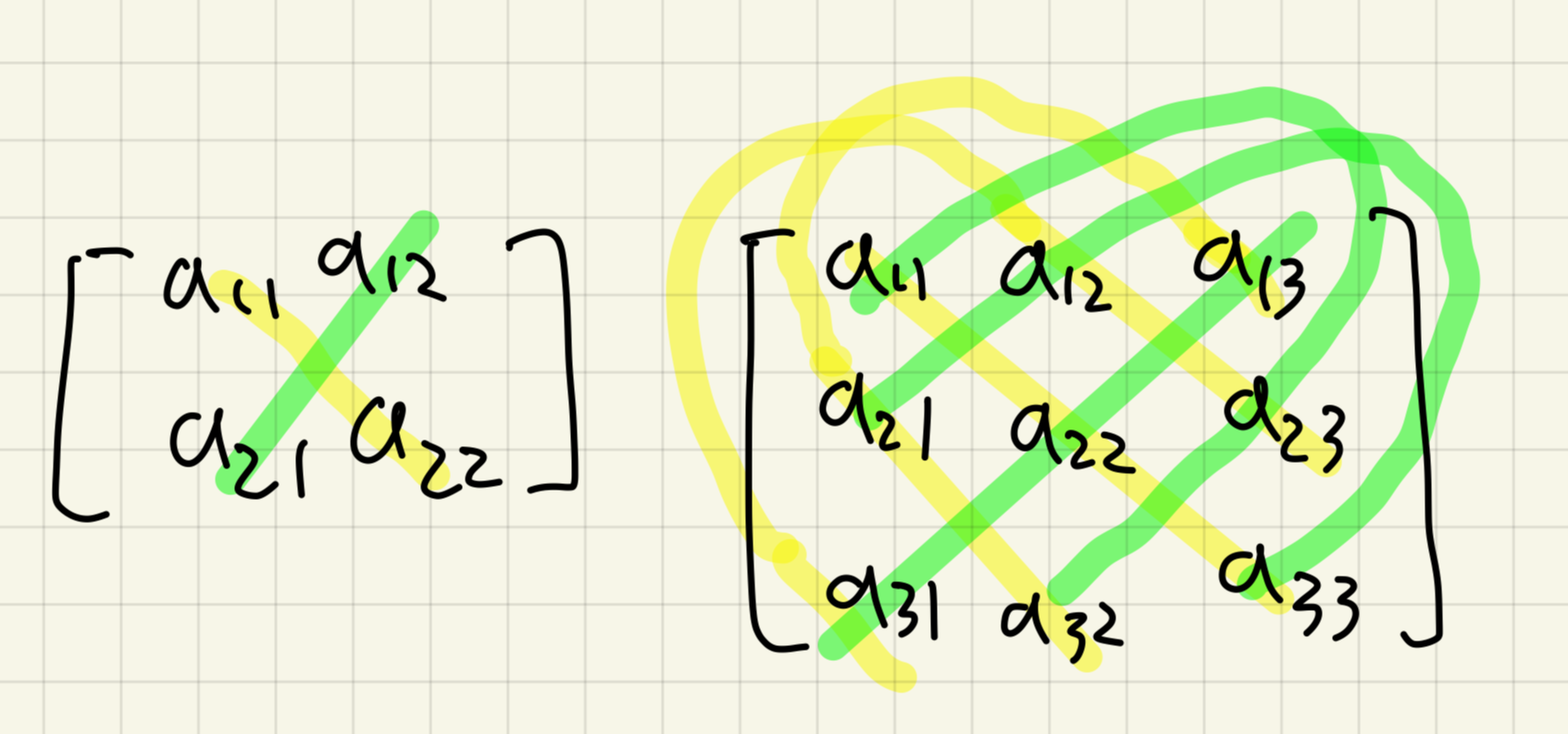
여인수에 의한 계산
사루스의 공식을 통해서 나온 3 x 3의 행렬식은 아래와 같이 인수분해될 수 있다:
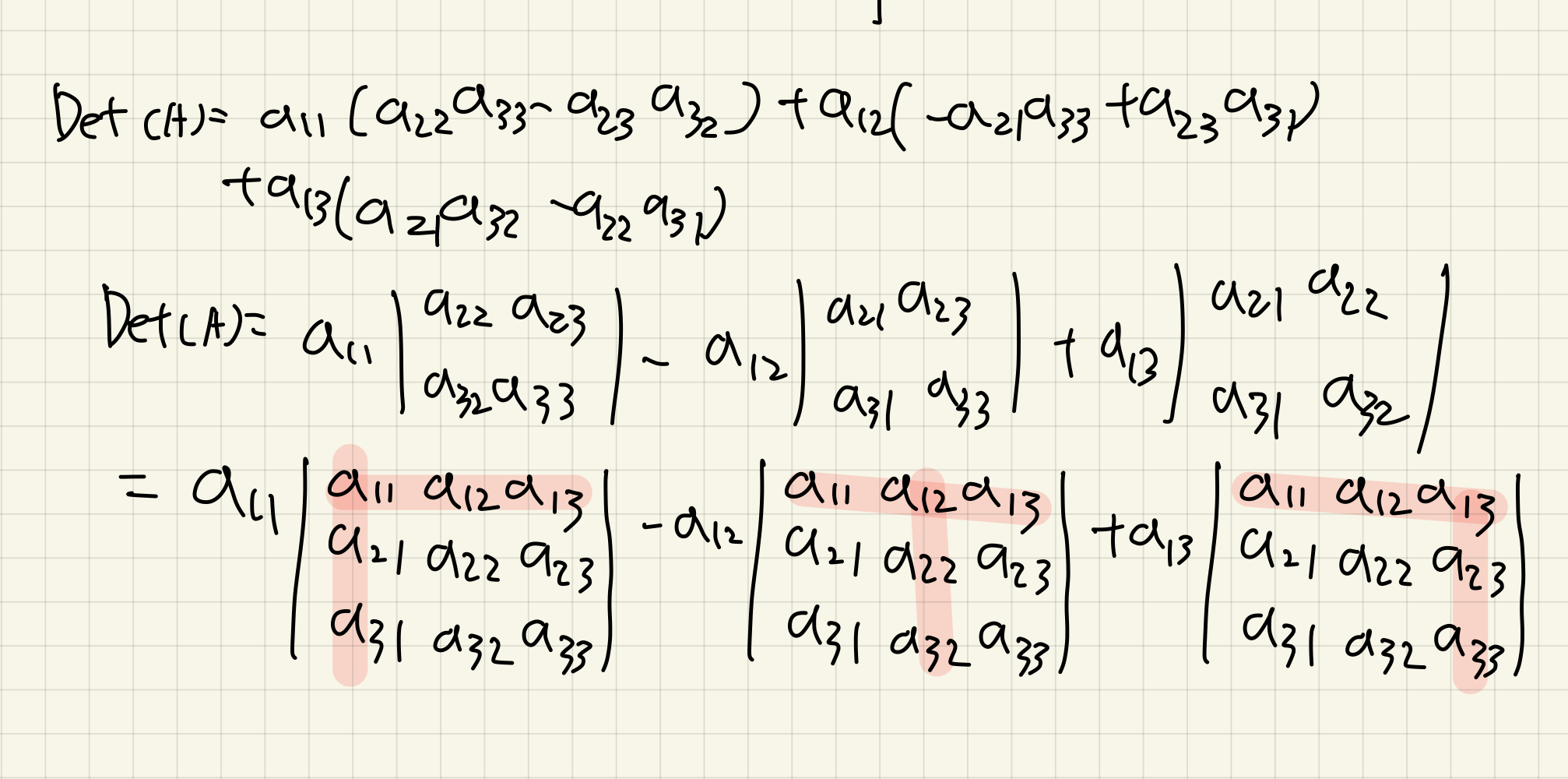
이는 행렬식에서 a11, a12, a13을 기준으로 해당하는 행과 열을 제외하고 연산을 하는 것과 같은 결과를 가져온다.
aij를 포함하는 행과 열을 제외한 나머지 행과 열로 이루어진 행렬식 Mij를 aij의 소행렬식(minor)으로 정의한다.
i행과 j열을 제거하여 얻어진 부분행렬의 행렬식이다.
따라서, 다음과 같이 표현될 수 있다.
Det(A) = a11M11 - a12M12 + a13M13
Mij에다가 i+j의 값에 따라서 부호를 넣은 Aij를 여인수라고 하는데,
Aij = (-1)i+jMij이다.
따라서,
Det(A) = a11A11 - a12A12 + a13A13
이 식을 제 1행에 대해 여인수들로 전개되었다라고 말한다.
여인수는 소행렬식에다가 부호를 붙인 것인데, i+j가 짝수이면 Aij = Mij, 홀수이면 Aij = -Mij이다.
3 x 3의 크기에서는 왼쪽, 4 x 4의 크기에서는 오른쪽의 부호를 가진다.

행렬식의 성질들
- n x n의 행렬에서 임의의 두 행 또는 두 열이 같으면 행렬식의 값은 0이다.
- n x n 행렬 A의 임의의 두 행(열)을 서로 바꾸어서 만들어진 행렬을 B라고 하면, Det(B) = -Det(A)이다.
- 행렬 A의 행렬식의 값은 전치행렬의 행렬식의 값과 같다. (Det(A) = Det(AT)
- A와 B의 크기가 같으면 곱의 행렬식은 행렬식의 곱과 같다. (Det(AB) = Det(A) * Det(B))
- 행렬식의 어떤 행(또는 열)의 각 원소에 같은 수 k를 곱하여 얻은 행렬식은 행렬식에 k를 곱한 것과 같다.
- n x n행렬 A의 한 행(열)에 있는 모든 원소가 0이면 Det(A) = 0이다.
- A가 n x n의 삼각행렬인 경우, Det(A)는 주대각선상의 원소들의 곱과 같다. (Det(A) = a11 x a22 x ... x ann)
- 삼각행렬이 가역적이기 위한 필요충분조건은 그 대각선상의 모든 성분들이 0이 아니어야 한다.
기본 행 연산을 통한 행렬식의 계산
행렬식의 크기가 커지면, 시간이 많이 걸린다.
따라서, 기본 행 연산을 통해서 행렬식의 성질을 활용하면 더욱 편리하게 행렬식의 값을 구할 수 있다.
- 한 개의 행(또는 열)에 k배를 한 행렬식은 원래 행렬식의 k배와 같다.
- 두 개의 행(또는 열)을 교환한 행렬식은 원래 행렬식에서 부호만 바뀐다.
- 한 개의 행(또는 열)에 k배를 하여 다른 행(또는 열)에 더하여 만든 행렬식은 원래의 행렬식과 같다.
기본 행 연산을 통해서 삼각행렬로 만들어버리면, 행렬식의 값을 빠르게 구할 수 있다!
연습문제
의 행렬식의 값을 구하시오.
풀이: 기본 행 연산과 행렬식의 성질을 이용하여 간편하게 구할 수 있다.

'수학 > 선형대수' 카테고리의 다른 글
| [선형대수] 4. 벡터 (0) | 2024.01.07 |
|---|---|
| [선형대수] 3-2. 역행렬과 선형시스템의 해 (0) | 2024.01.06 |
| [선형대수] 2-2. 특수한 행렬과 기본 행 연산 (0) | 2024.01.04 |
| [선형대수] 2-1. 행렬, 행렬의 연산 (0) | 2024.01.03 |
| [선형대수] 1-2. 선형방정식의 소거 (0) | 2024.01.02 |




