넘치게 채우기
[선형대수] 2-1. 행렬, 행렬의 연산 본문
행렬은 수 또는 문자를 행과 열에 맞추어 구성한 직사각형 배열이다.
m x n행렬 또는 (m, n)행렬이라고 부른다.
이 행렬은 m개의 행(row)와 n개의 열(column)을 가진다.

aij를 ij-항이라고 한다. i번째 행과 j번째 열이 만나는 항의 값이다.
행렬의 각 행은 가로의 n순서쌍으로, 각 열은 세로의 m순서쌍으로 볼 수 있다.
가로의 n 순서쌍을 행벡터(row vector), 세로의 m 순서쌍을 열벡터(column vector)라고 한다.

정방행렬
행렬의 행의 개수와 열의 개수가 모두 같은 경우, m=n인 경우가 있는데, 이를 정방행렬(square matrix)라고 한다.
n개의 행과 n개의 열을 가지는 행렬을 n차 정방행렬(square matrix of order n)이라고 한다.
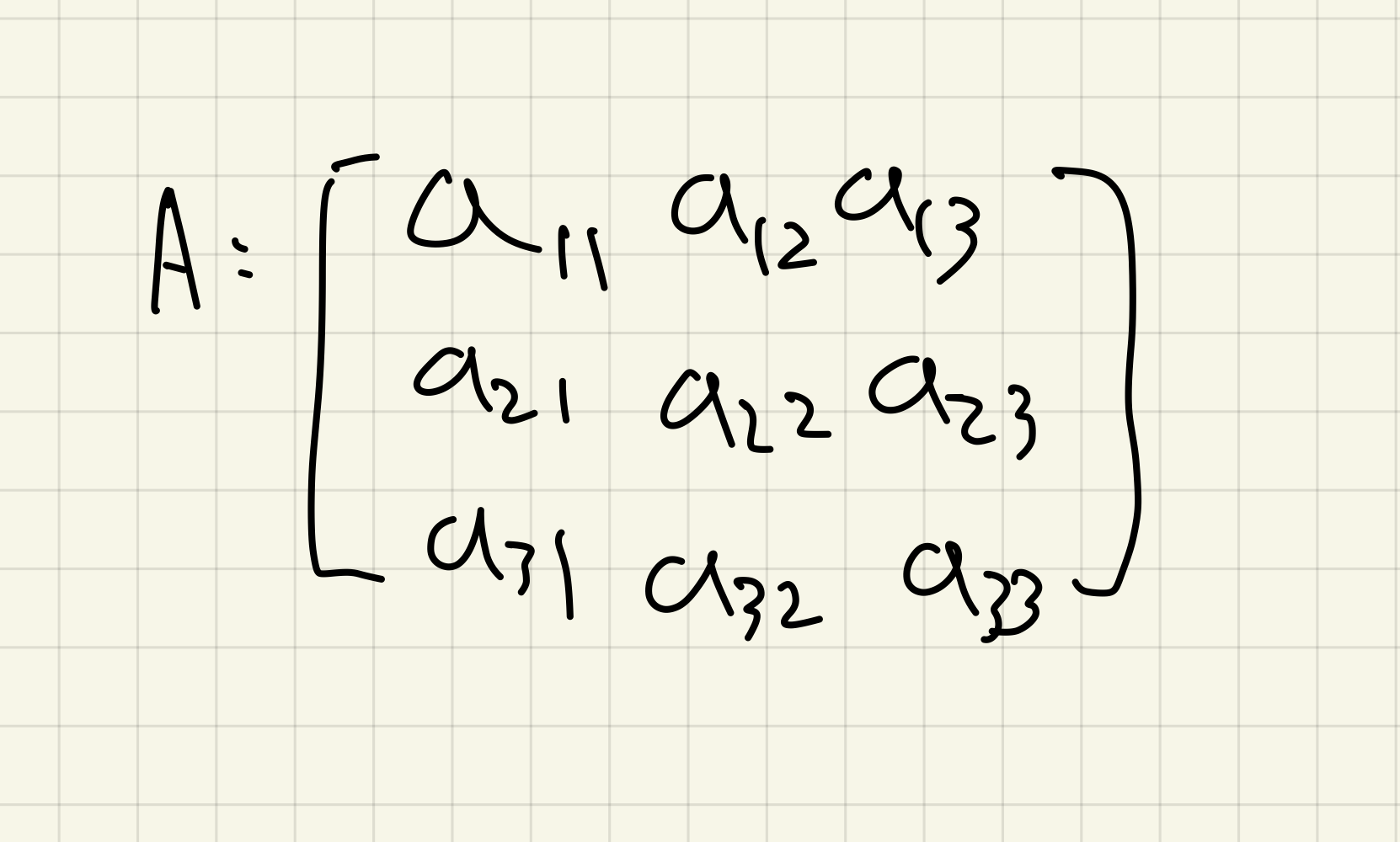
행렬의 합
행렬의 합은 크기가 같은 행렬일 때에 한해 정의된다. 즉, 행렬 A, B가 모두 m x n의 행렬이라고 할 때,
행렬의 합 A+B는 각 ij-성분의 합을 ij성분으로 하는 행렬로 정의한다.

행렬의 차
행렬의 차 역시 크기가 같아야 한다.
A - B 또는 A + (-1)B라고 쓰고, A에서 B를 뺀 차(difference)라고 한다.
A의 각 ij-요소에 B의 각 ij-요소를 뺀 값을 ij-요소로 한다.

스칼라 곱
행렬의 스칼라 곱은 다음과 같다:
k가 실수 값이고, 임의의 행렬 A가 있다고 할 때, kA는 행렬 A의 각 성분에 k를 곱한 값을 말한다.

행렬의 연산법칙
같은 크기의 행렬 A, B, C, 어떤 상수 c, d가 있다고 할 때, 다음의 연산법칙들을 만족한다.
- A + B = B + A (덧셈의 교환법칙)
- (A + B) + C = A + (B + C) (덧셈의 결합법칙)
- A + O = O + A (덧셈의 항등법칙)
- A + (-A) = (-A) + A = O (덧셈의 역원)
- c(A + B) = cA + cB (스칼라 곱의 배분법칙)
- (c+d)A = cA + dA (스칼라 곱의 배분법칙)
행렬의 곱
행렬 A가 m x n행렬이고, B가 n x p행렬일 때, 행렬 A와 B의 행렬의 곱은 AB = C = [cij]로, 다음과 같이 정의된다.
A의 열의 숫자가 B의 행의 숫자가 같을 경우에 정의된다.
또한, C의 (i, j)항들은 A의 i번째 행과 B의 j번째 열을 곱한 합으로 만들어진다는 점에 유의한다.
A가 m x n행렬, B와 C는 행렬의 합과 곱에서 정의된 크기를 만족하고, k가 어떤 스칼라 값일 때, 다음의 법칙이 성립한다:
- A(BC) = (AB)C (곱셈의 결합법칙)
- A(B+C) = AB + AC (왼쪽 배분법칙)
- (B+C)A = BA + CA (오른쪽 배분법칙)
- k(AB) = (kA)B = A(kB) (스칼라 곱)
- I[n]A = A = AI[n] (행렬 곱셈의 항등식)
교환법칙은 성립하지 않는다.
행렬의 거듭제곱
정방행렬 A(n*n)과 양의 정수 k가 있을 때, A^k는 A를 k번 곱한 것이다.
A^k = A^(k-1) * A, A^0 = I(항등행렬. 주대각선의 항만 1, 나머지는 0)
부행렬
행렬은 분할이 가능하다.
아래는 4 x 4의 행렬 A를 4개의 부행렬(submatrix)로 나눈 예시이다.

연습문제
1.

2.

'수학 > 선형대수' 카테고리의 다른 글
| [선형대수] 3-2. 역행렬과 선형시스템의 해 (0) | 2024.01.06 |
|---|---|
| [선형대수] 3-1. 행렬식과 여인수 (0) | 2024.01.05 |
| [선형대수] 2-2. 특수한 행렬과 기본 행 연산 (0) | 2024.01.04 |
| [선형대수] 1-2. 선형방정식의 소거 (0) | 2024.01.02 |
| [선형대수] 1-1. 선형대수와 선형시스템 (0) | 2024.01.01 |




