넘치게 채우기
[선형대수] 1-1. 선형대수와 선형시스템 본문
선형대수
선형대수학은 선형방정식을 풀기 위한 수학적인 도구로써, 기하학의 문제를 효과적으로 해결하기 위한 방법론이다.
최근 인공지능에서 중요한 역할을 담당한다.
선형이란
선형(Linear)이란 집합 A의 원소들에 대하여 각각 선형결합의 형태로 나타낼 수 있는 것을 말한다.
즉, 집합 A의 원소 x1, x2, x3, ... xn에 대하여 각각 상수 a1, a2, a3, ..., an을 곱하여 더한 a1x1 + a2x2 + ... + anxn이 집합 A에 속하는 경우를 말한다.
(대응하는 계수와 변수를 모두 곱하고 그 값들을 모두 합한 값)
1차함수와 벡터 등은 선형을 나타내는 선형함수이다.
반대로, 2차 이상의 함수, 삼각 함수 등은 비선형함수라고 한다.
| 선형(Linear) | 비선형(Nonlinear) |
| 1차식, 1차함수 | 1차식이 아닌 2차 이상의 함수거나 cos(x)등의 함수 |
| 하나의 원인 -> 하나의 결과 | 훨씬 복잡함 |
| 직선 그래프 | 곡선 그래프 |
| 속도와 거리의 관계 | 카오스 |
| 행렬로 표현 가능 | 행렬로 표현 불가능 |
선형방정식
a1x1 + a2x2 + ... + anxn = b 와 같은 방정식을
변수(variable) x1, x2, ..., xn과
계수(coefficient) a1, a2, ... , an에 관한 선형방정식(linear equation)이라고 한다.
이러한 등식을 성립시키는 변수 x1, x2, ... , xn의 값을 해(solution)이라고 한다.
선형시스템
변수 x1, x2, ... , xn에 대해서 유한개의 선형방정식의 집합을 선형시스템(linear system)이라고 한다.
선형시스템의 모든 해의 집합을 해집합(solution set)이라고 한다.

선형방정식의 해
해가 있다(consistent) - 방정식을 만족시키는 경우의 해가 있는 경우
해가 없다(inconsistent) - 방정식을 만족시키는 경우의 해가 없는 경우
만약 모든 상수항이 0인 경우(위 그림에서 b1, b2, ..., bn이 모두 0인경우), 동차선형시스템(homogeneous system)이라고 한다.
x1 = x2 = ... = xn = 0인 경우 항상 해가 된다. 이러한 경우의 해를 자명해(trivial solution)라고 한다.
만약 변수 중 하나라도 0이 아닌 경우의 해가 있다면, 그 해를 비자명해(nontrivial solution)라고 한다.
선형방정식들이 똑같은 해를 가진 경우, 두 식이 동치(equivalent)한다고 한다.
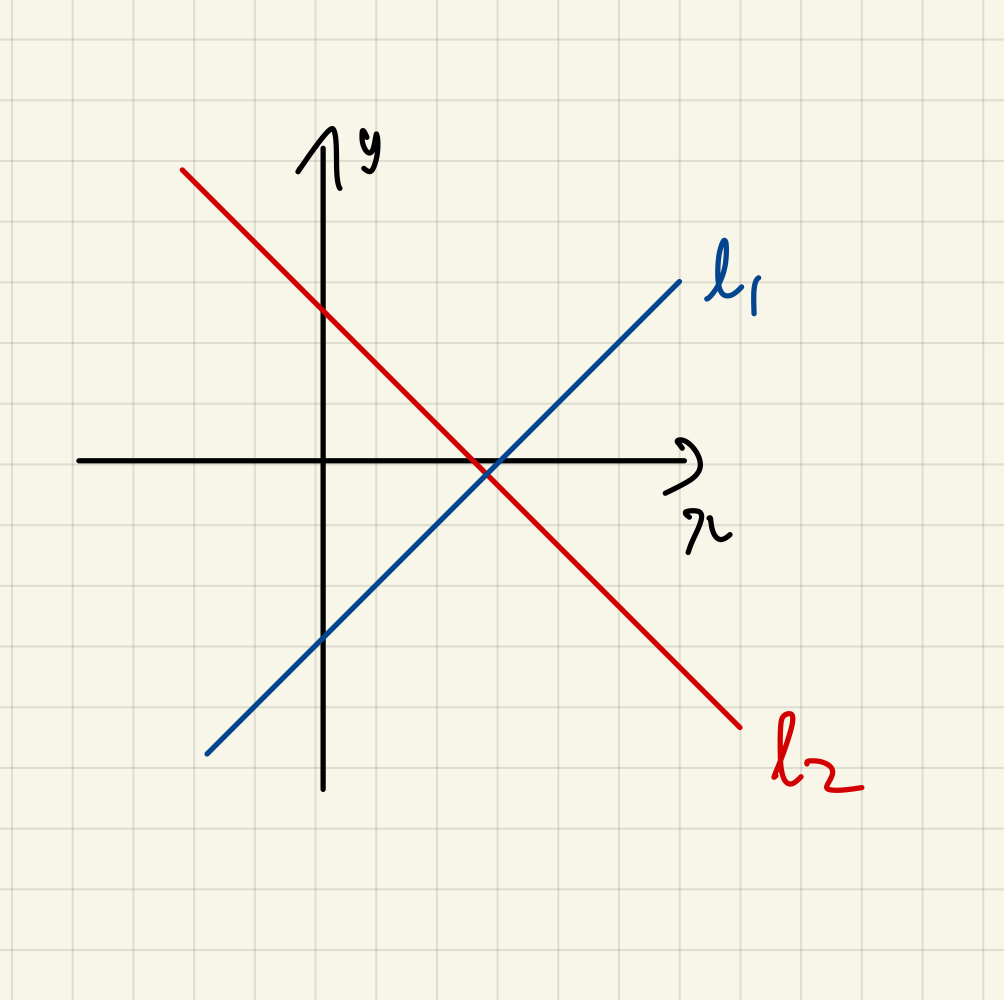
선형방정식의 해를 기하학적으로 표현하면 다음과 같다:
유일한 해)
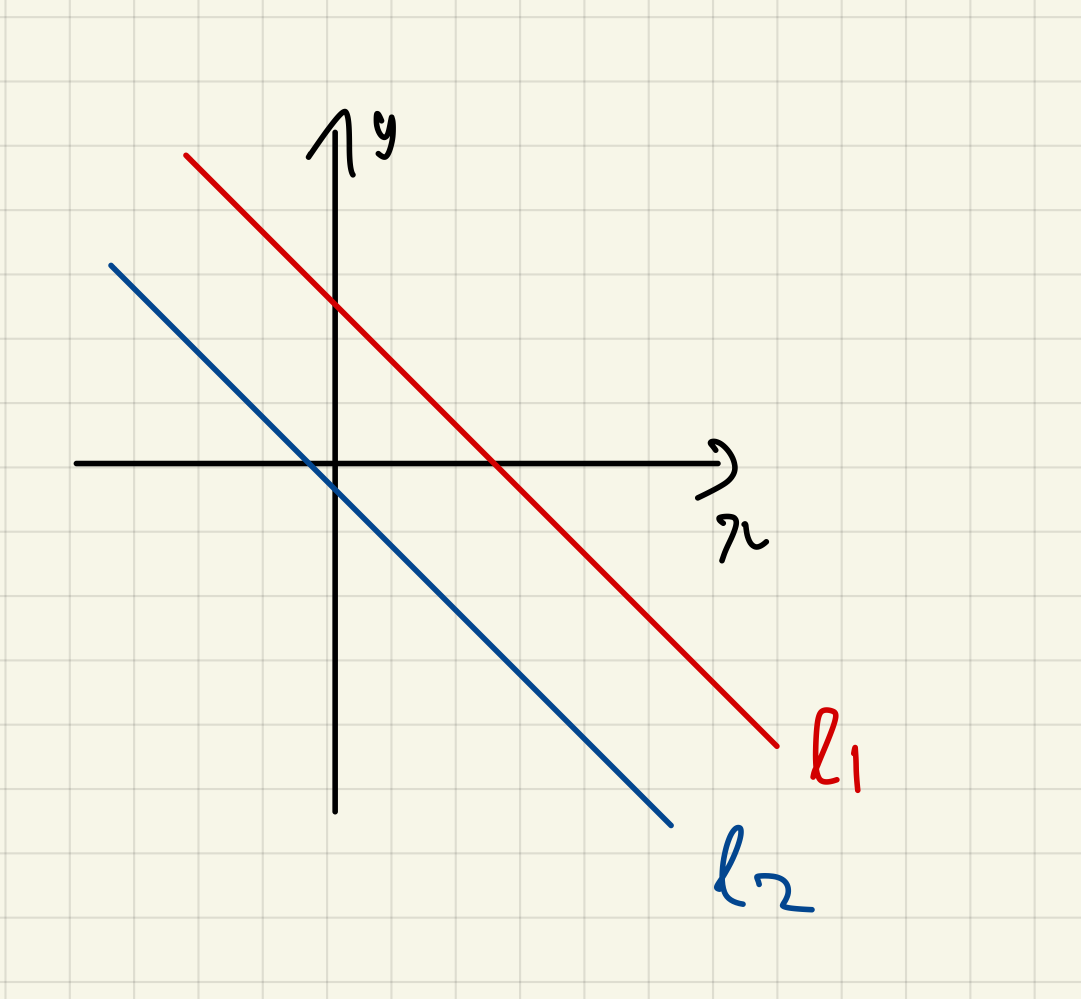
해가 없음)
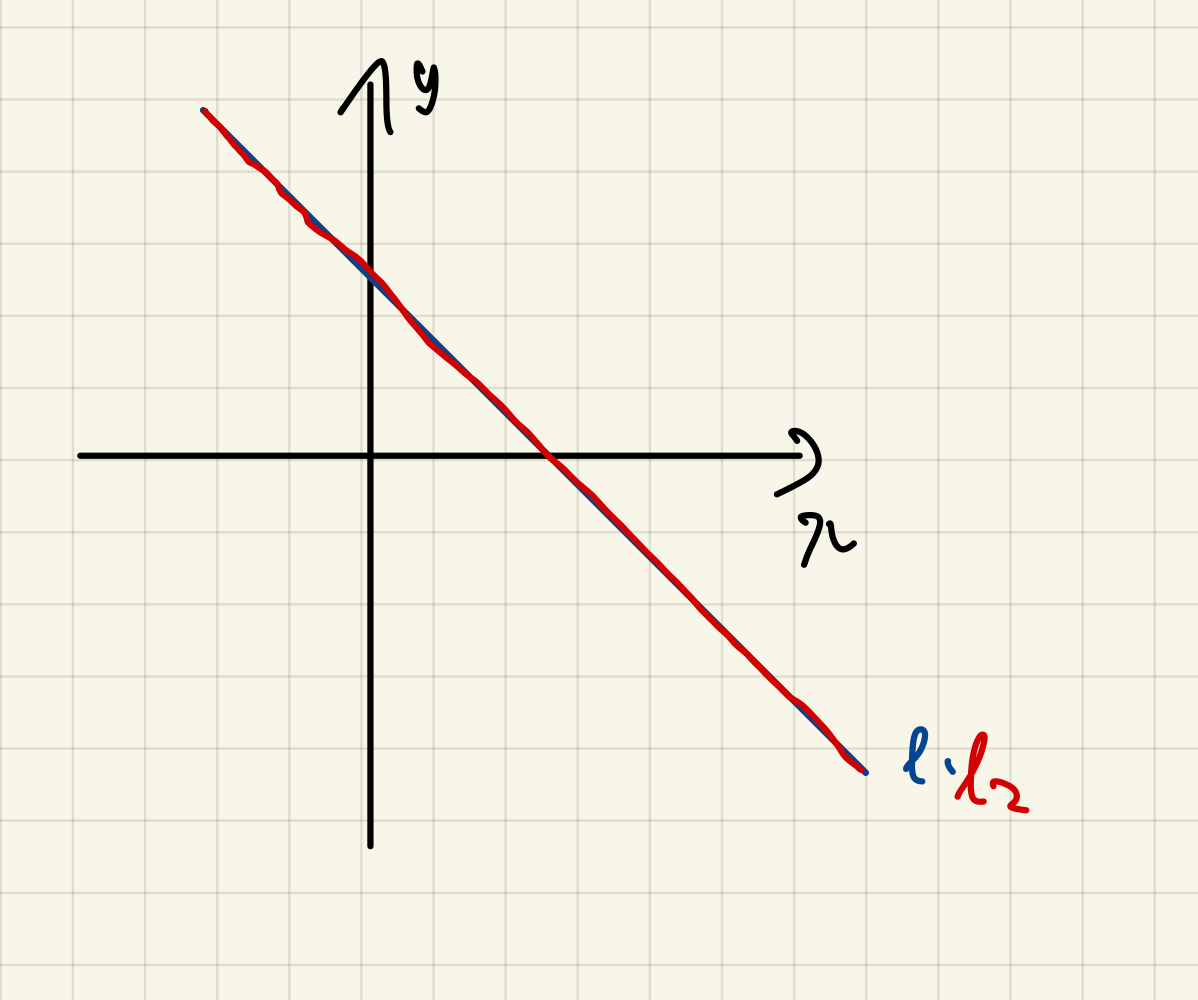
해가 무한히 많음)
연습문제)
2x1 - x2 = 3
-4x1 + 2x2 = -6의 해의 개수는?
답: 해가 무한히 많다.

'수학 > 선형대수' 카테고리의 다른 글
| [선형대수] 3-2. 역행렬과 선형시스템의 해 (0) | 2024.01.06 |
|---|---|
| [선형대수] 3-1. 행렬식과 여인수 (0) | 2024.01.05 |
| [선형대수] 2-2. 특수한 행렬과 기본 행 연산 (0) | 2024.01.04 |
| [선형대수] 2-1. 행렬, 행렬의 연산 (0) | 2024.01.03 |
| [선형대수] 1-2. 선형방정식의 소거 (0) | 2024.01.02 |




