넘치게 채우기
[선형대수] 7. 선형변환 본문
선형변환의 정의
V와 W가 벡터공간이고, u, v가 V에 속하며 a가 실수인 경우, V로부터 W로가는 함수 L이 아래 2가지를 만족할 때, 선형변환(linear transformation)또는 선형사상(linear mapping)이라고 한다.
L: V->W
- L(u+v) = L(u) + L(v)
- L(au) = aL(u)
특히 V = W일 경우에는 선형변환 L을 V상에서의 선형연산자(linear operator)라고 한다.
L(x) = 2x는 선형변환인가?
L(x+y) = 3(x+y)
=3x+3y
=L(x)+L(y)
L(ax) = 3(ax)
=a(3x)
=aL(x)
선형변환이다.
함수와 선형변환
집합 X에서 집합 Y로의 관계의 부분집합으로써, 집합 X의 모든 원소 x가 집합 Y에 있는 원소 중 한 개와 관계가 있을 경우 f를 함수(function)라고 하며 다음과 같이 나타낸다.
여기서 X를 함수의 정의역(domain)이라고 하며, Y를 함수 f의 공변역(codomain)이라고 한다.
일때, y를 함수 f에 대한 x의 상(image)또는 함수값이라고 한다.
이러한 경우의 y들의 집합을 치역(range)이라고 한다.
단사함수, 전사함수, 전단사함수
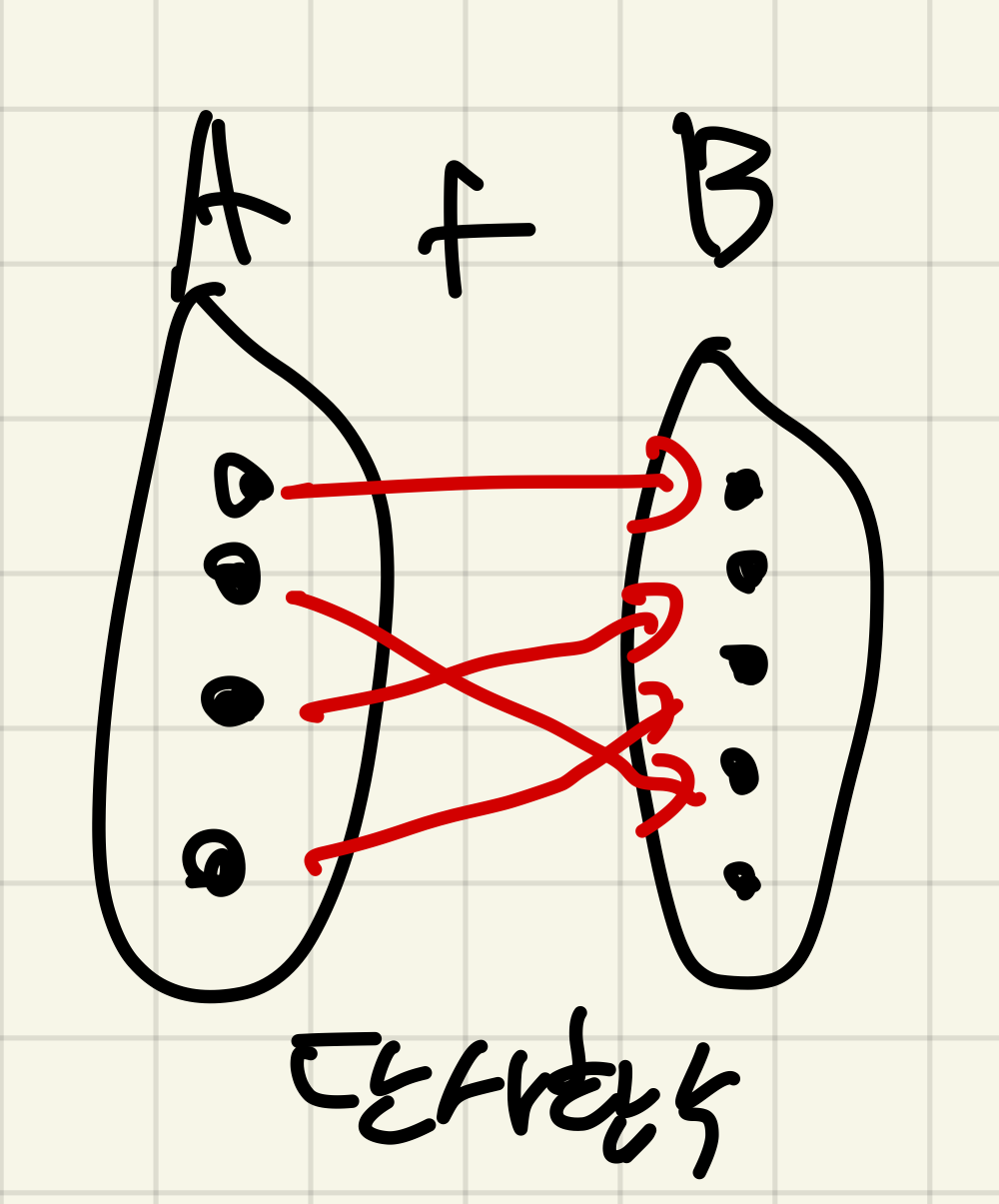
단사함수)
에 대하여
f(ai) = f(aj)일때 ai=aj인 경우를 단사함수(injective function)이라고 한다.
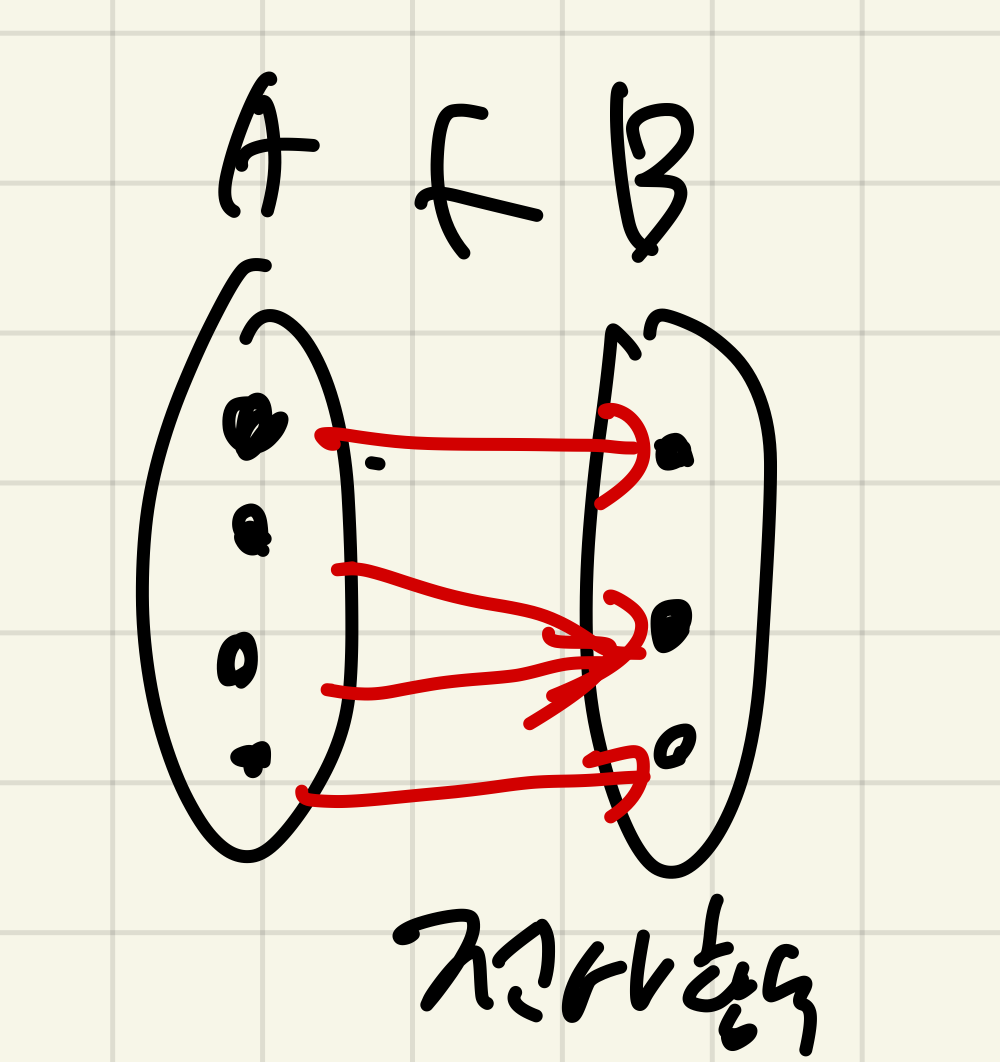
전사함수)
함수 f: A -> B에 대해서 B의 모든 원소 b에 대해 f(a) = b가 성립되는
가 적어도 하나 존재할 때, 함수 f를 전사함수(surjective function, onto function)라고한다.
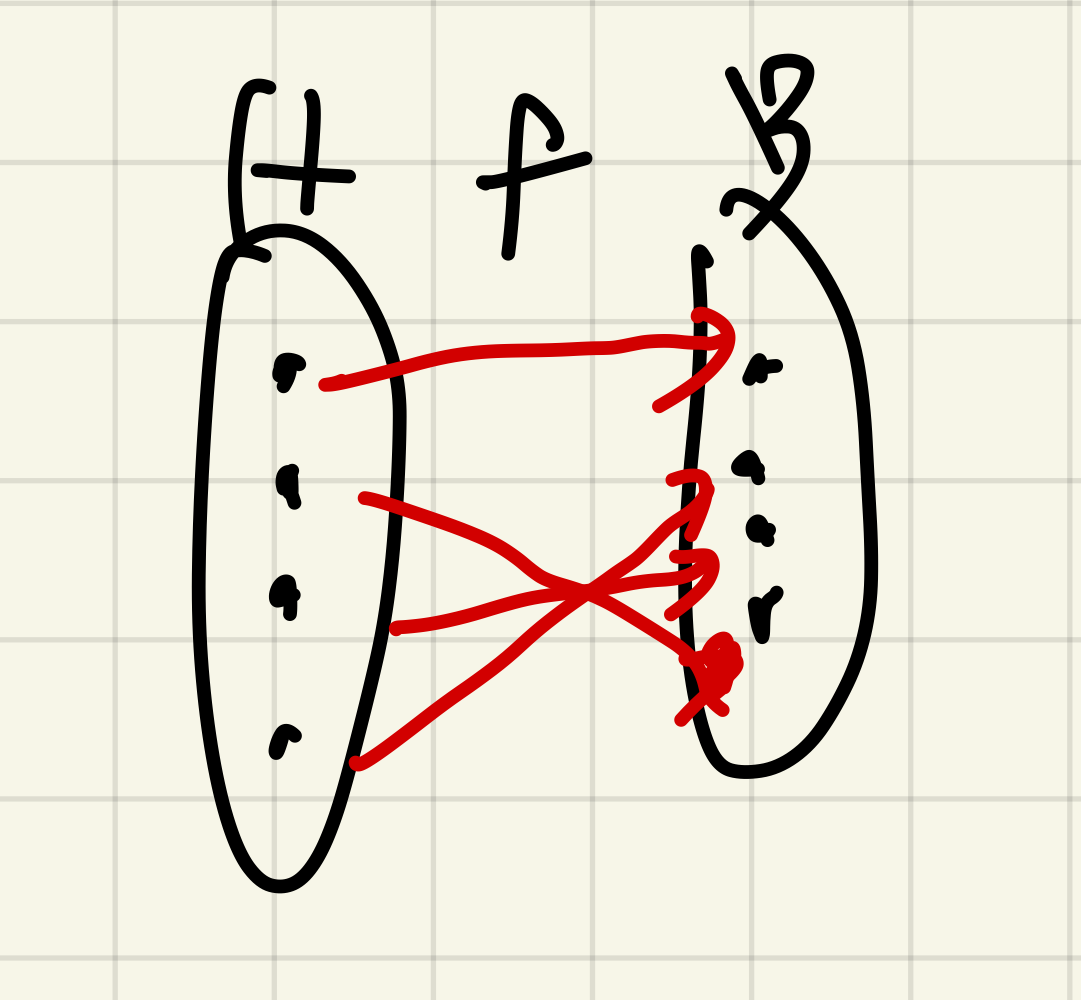
전단사함수)
함수 f: A->B가 단사함수이고 전사함수인 경우 전단사함수(bijective function)라고 한다.
이 전단사 함수는 집합 A의 모든 원소들이 집합 B의 모든 원소와 하나씩 되응되기 때문에 1대1 대응함수(one-to-one correspondence)라고도 한다.
합성함수
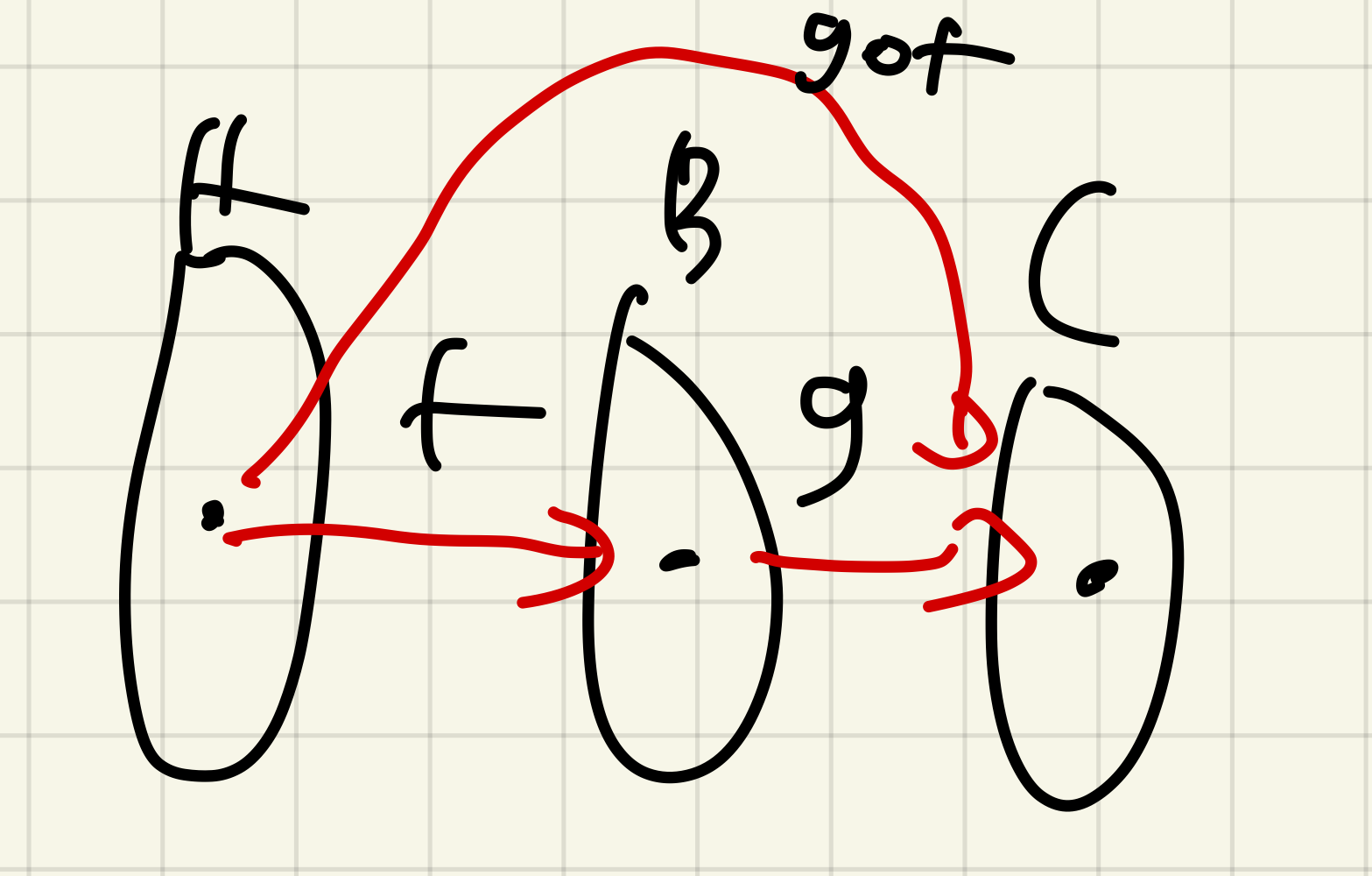
두 함수
에 대하여 두 함수 f와 g의 합성함수는 집합 A에서 집합 C로의 함수인
를 의미하며 다음을 만족한다.
함수 f의 공변역은 함수 g의 정의역이 된다. 함수 f, g와 합성함수 g·f에 대한 관계는 아래와 같다:
입력 값과 출력 값이 모두 벡터인 함수를 변환(transformation)이라고 하는데, 통상 대문자 L, T, F등으로 표시한다.
L이 벡터 x로부터 벡터 w로 보내는 변환일 경우 L(x) = w로 표현한다.
합성함수의 선형변환은 (L1·L2)(a)와 같이 표현하며, 순서에 따라 사영, 확대, 반사, 회전 등의 선형연산이 진행될 수 있다.
만약 L: V -> W가 벡터공간 V에서 W로의 선형변환이라고 할 때, ker(L)로 나타내는 L의 커널(kernel)은
L(v) = 0을 만족하는 V의 부분집합 요소들이다.
여러 가지 선형변환
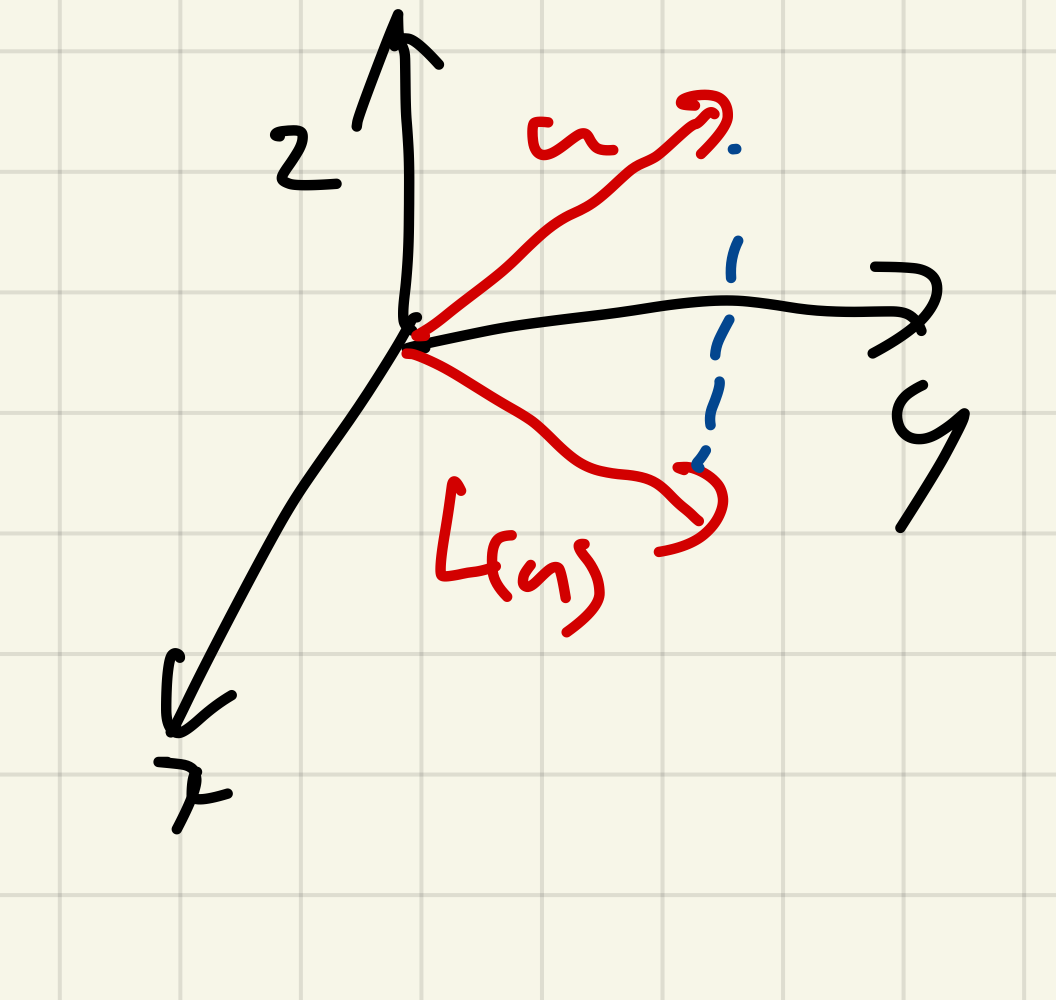
사영변환
사영변환(projection transformation): 한 차원 낮은 공간에 수직으로 사영시키는 변환이다.
아래는 사영의 예와, 사영이 선형변환이 되는지 확인하는 과정이다.
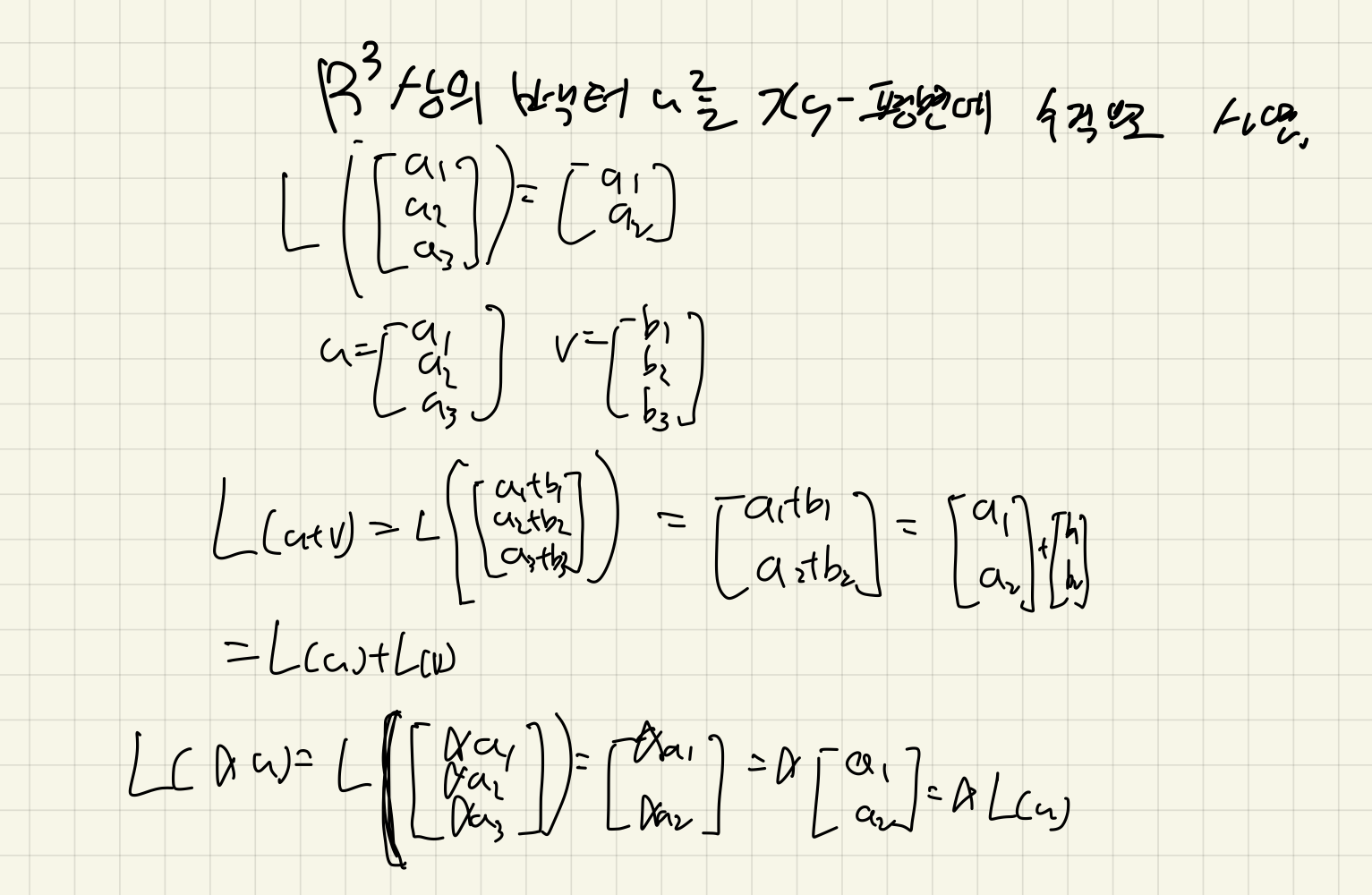
확대변환과 축소변환
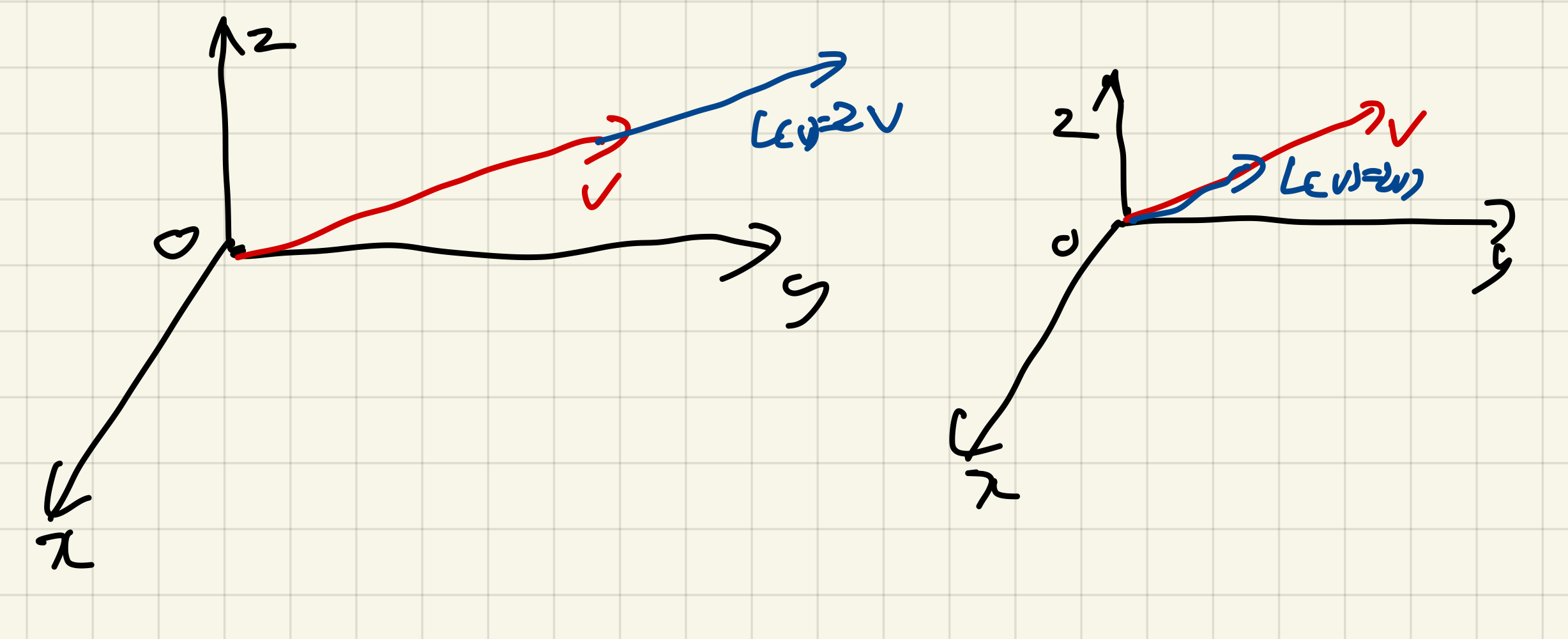
확대변환(dilation transformation), 축소변환(contraction transformation): 벡터의 길이를 늘리거나 줄이는 변환
r > 1인경우 확대변환이고,
0 < r < 1인 경우 축소변환이다.
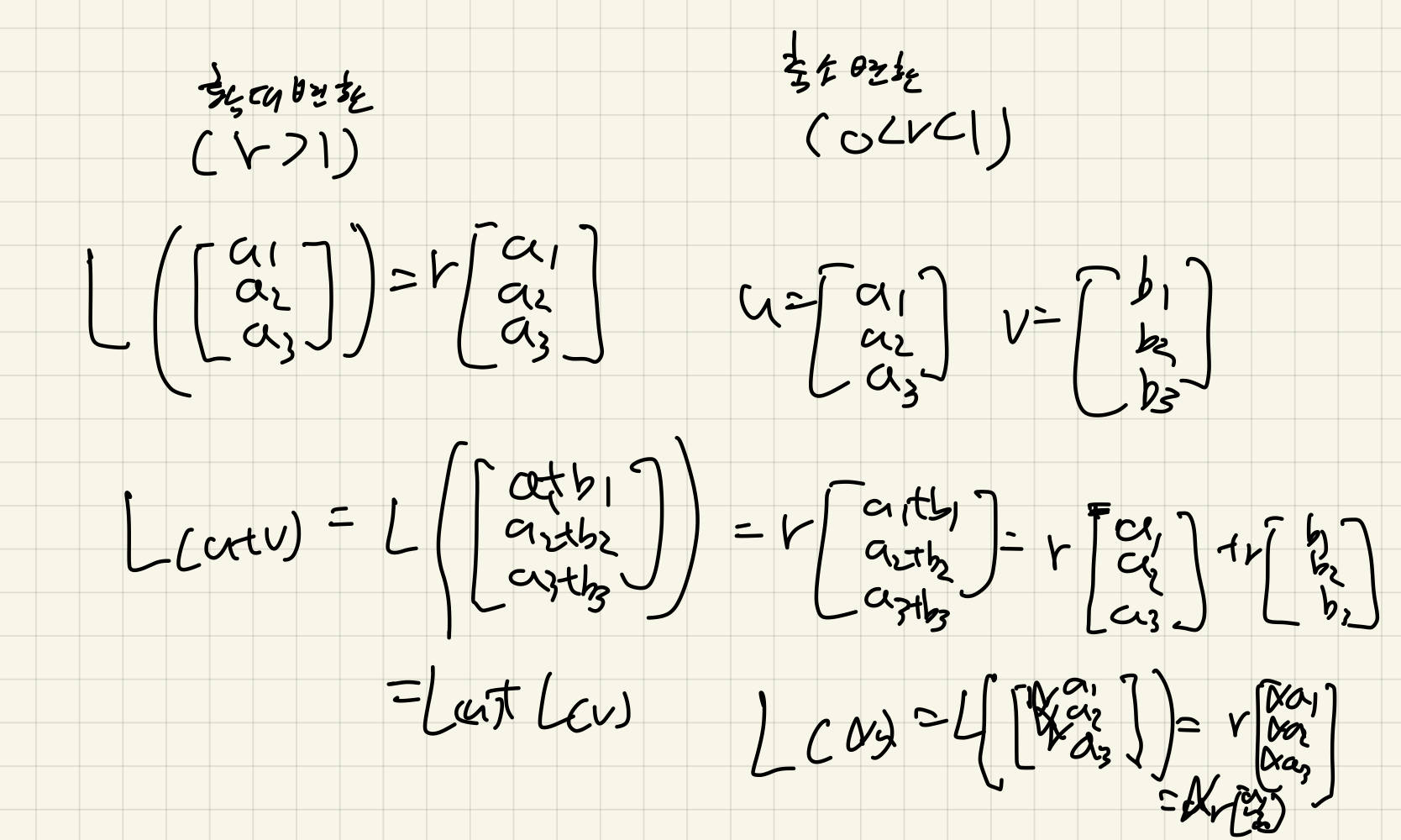
반사변환
반사변환(relfection transformation): 특정 축에 대해서 대칭이 되도록 선형변환
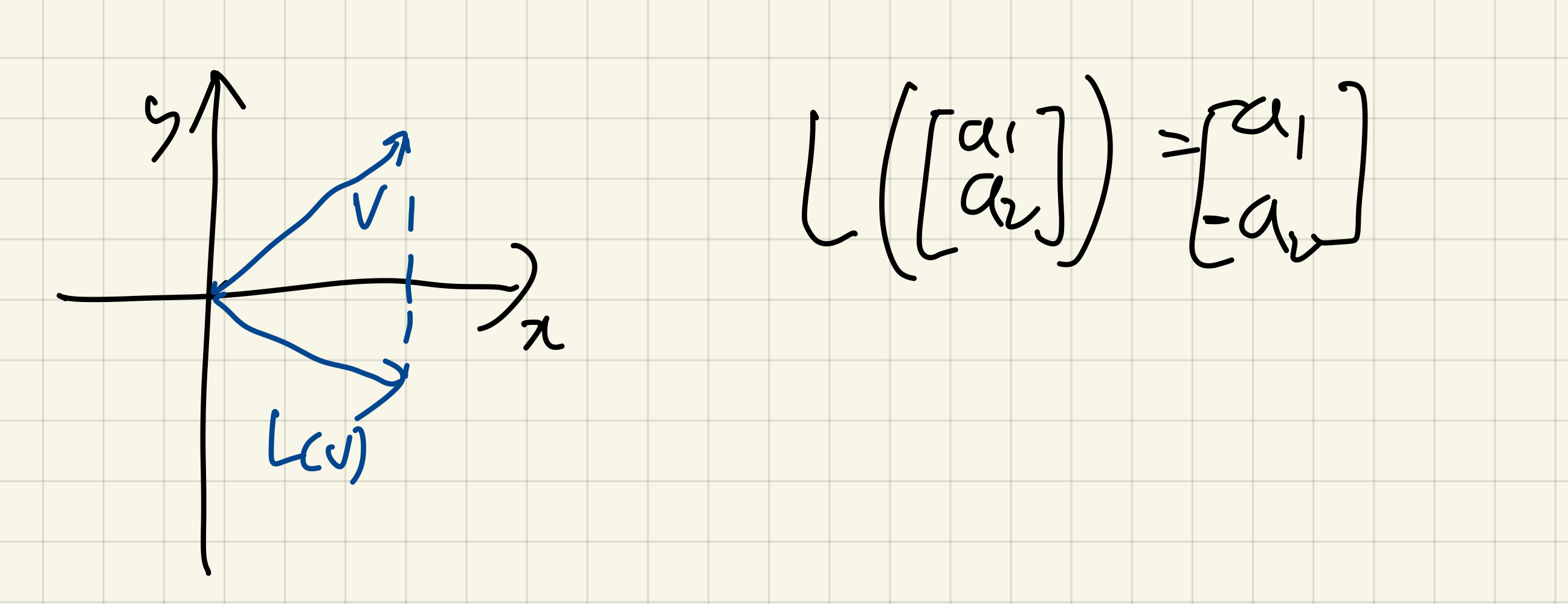
회전변환
회전변환(rotation transformation): 원점 O를 중심으로 특정 각도만큼 회전된 벡터
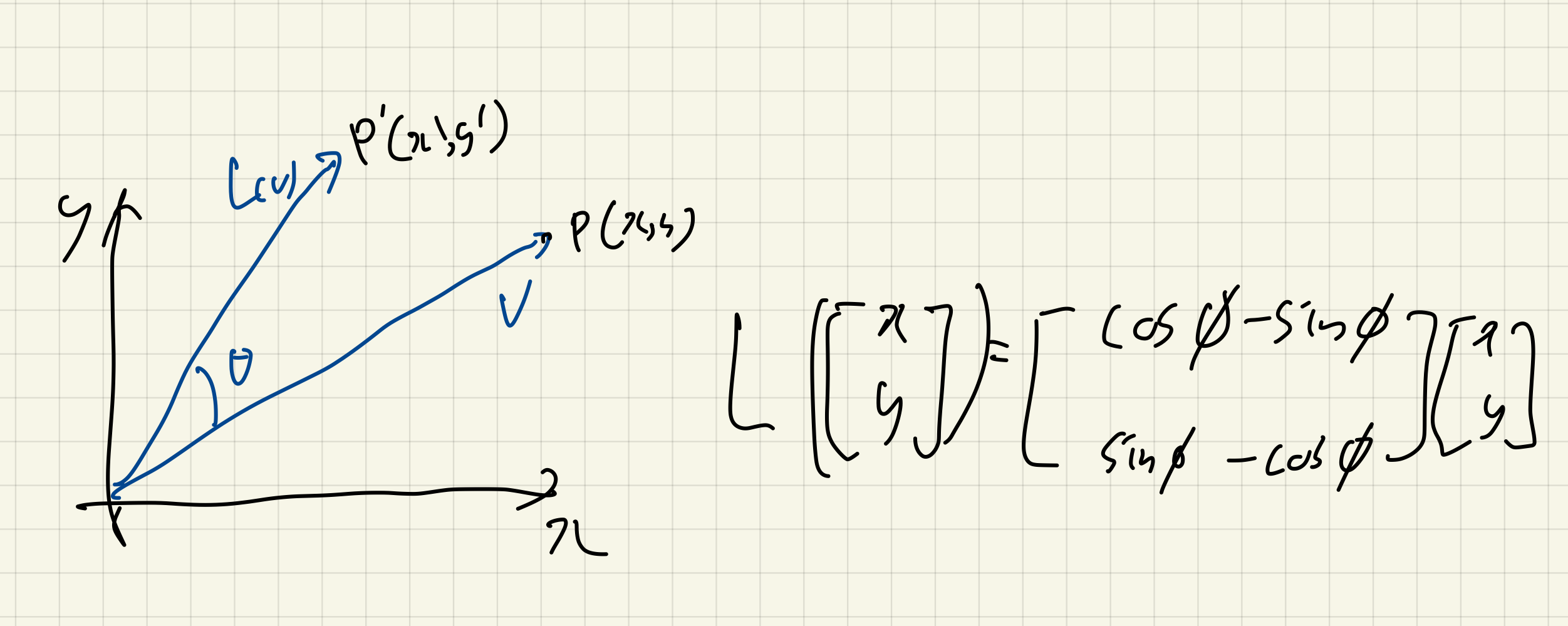
변환의 표준행렬
L: Rn => R1이 선형변환일 때, {e1, e2, ..., en}이 Rn에서의 표준기저라고 하고, A가 m x n행렬이고 j번째 열이 L(ej)라고 하자.
만약 x = (x1, x2, ..., xn)이 Rn상의 어떤 벡터라고 하면 행렬 A는
L(x) = Ax인 성질을 가진다.
더군다나 A가 위의 식을 만족하는 유일한 행렬일 때, A를 L를 나타내는 표준행렬(standard matrix)이라고 한다.
아래는 R2상의 대표적인 표준행렬 예시이다.
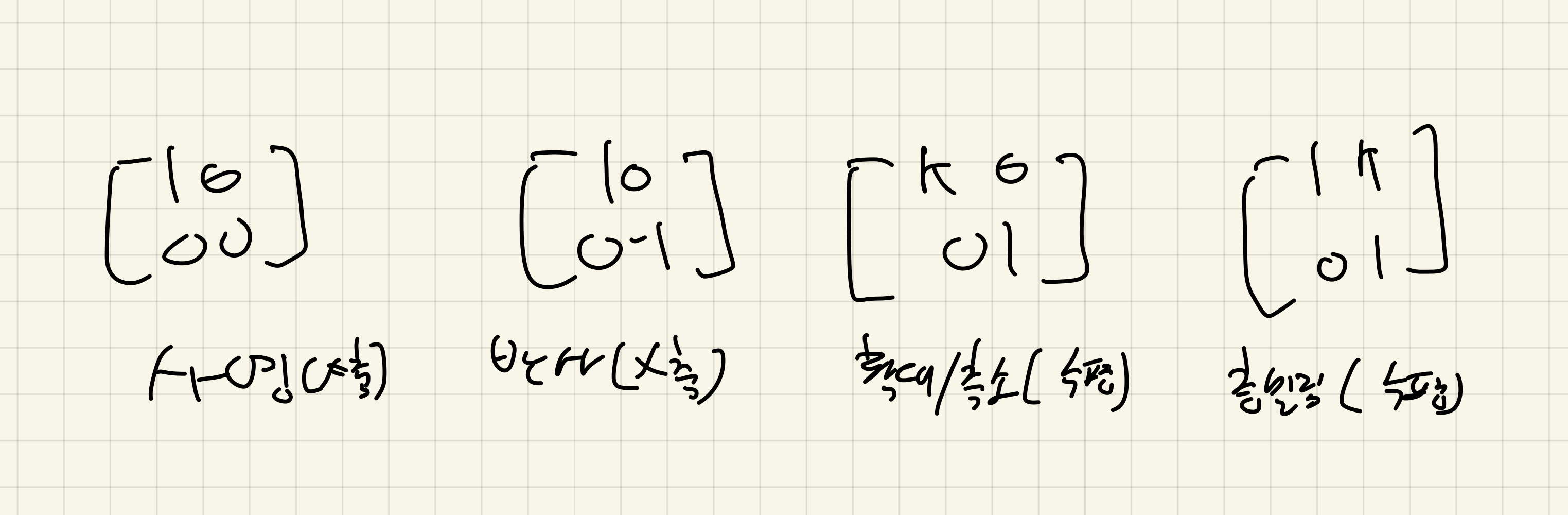
'수학 > 선형대수' 카테고리의 다른 글
| [선형대수] 6-2. 외적 (0) | 2024.01.11 |
|---|---|
| [선형대수] 6-1. 벡터의 내적 (0) | 2024.01.10 |
| [선형대수] 5-2. 생성, 기저, 차원 (0) | 2024.01.09 |
| [선형대수] 5-1. 벡터공간 (0) | 2024.01.08 |
| [선형대수] 4. 벡터 (0) | 2024.01.07 |




