넘치게 채우기
[선형대수] 6-1. 벡터의 내적 본문
내적의 정의
u, v가 Rn상의 벡터라고 할 때, Rn상의 내적(inner product, dot product)은
다음과 같은 스칼라 값으로 나타내고, u·v로 나타낸다.
이는 각 대응하는 요소들의 곱의 합이다.

내적이 음수면 두 벡터가 반대방향임을, 0이면 직교함을 의미한다.
내적을 통해 인공지능에서의 신경망에서의 입력과 연결강도와의 곱을 효율적으로 수행할 수 있다.
두 벡터 사이의 거리 구하기
벡터의 노름은
, 두 벡터 u-v의 거리는
이다.
u = (1, 2, 3), v = (-4, 3, 5)의 거리는?
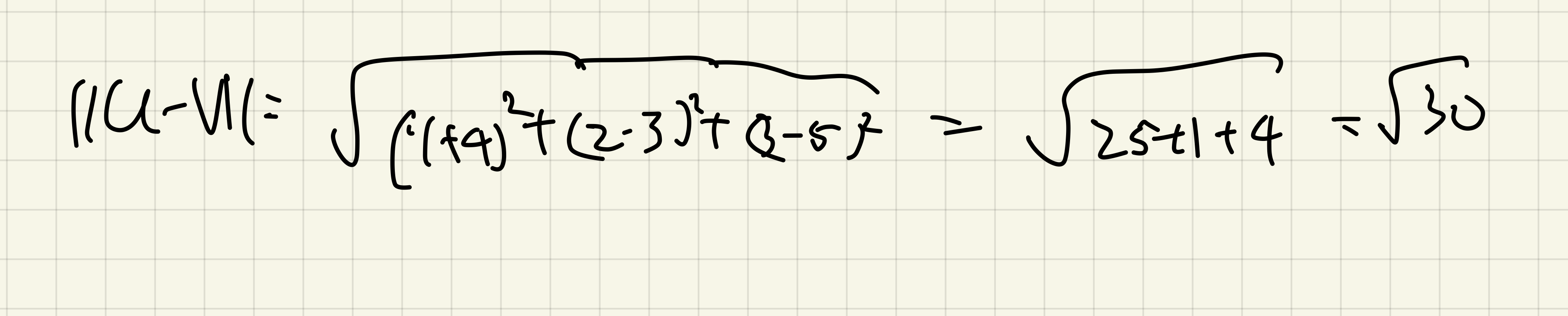
두 벡터 u,v가 이루는 각을 Θ라고 할 때, u와 v의 내적은 다음과 같다:
- u = 0 또는 v = 0인경우, u·v = 0
- u != 0 이고 v != 0 인 경우, u·v = ||u||||v||cosΘ
cosΘ = u·v / (||u||||v||)이다.(단, u != 0 이고 v != 0)
u = (1,1,0), v = (0, 1, 1)인 경우의 사이 각을 구해보자.
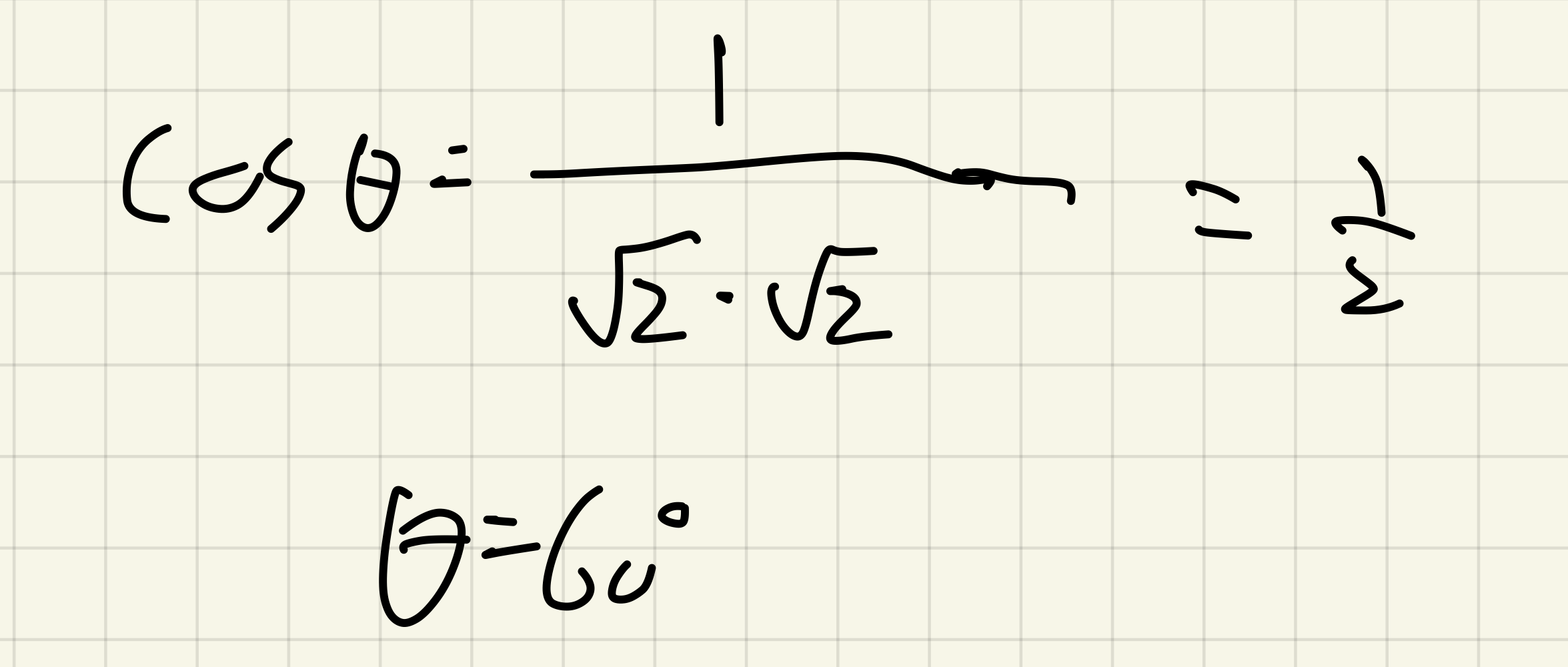
피타고라스 정리
두 벡터 u와 v가 수직일 필요충분조건은
||u+v||2 = ||u||2 + ||v||2이다.
내적의 성질과 직교
u, v, w가 R2나 R3의 벡터이고, c를 스칼라라 할 때, 다음의 성질을 가진다.
- u·u >= 0
- u·v = v·u
- (u+v)·w = u·w + v·w
- u·(v+w) = u·v+u·w
- cu·v = c(u·v)
- u·0 = 0·u = 0
- u·u = ||u2||
이를 만족하는 벡터공간을 내적 공간(inner product space)라고 한다.
내적공간 V에서 두 벡터 u·v = 0이면, 직교(orthogonal)또는 수직하라고 한다.
u·v >0 이면 예각, u·v < 0이면 둔각을 가진다.
정규직교집합
Rn의 벡터들이 집합 S = {v1, v1, ..., vk}가 다음 성질을 만족시킬 때, 정규직교집합이라고 한다.
- vi·vj = 0(i != j)
- vi·vi = 1
1번만 만족하는 경우를 직교집합이라고 한다.
S = {v1, v1, ..., vk}가 영벡터가 아닌 직교집합이면 집합 S는 선형독립이다.
증명은 아래에서 볼 수 있다.
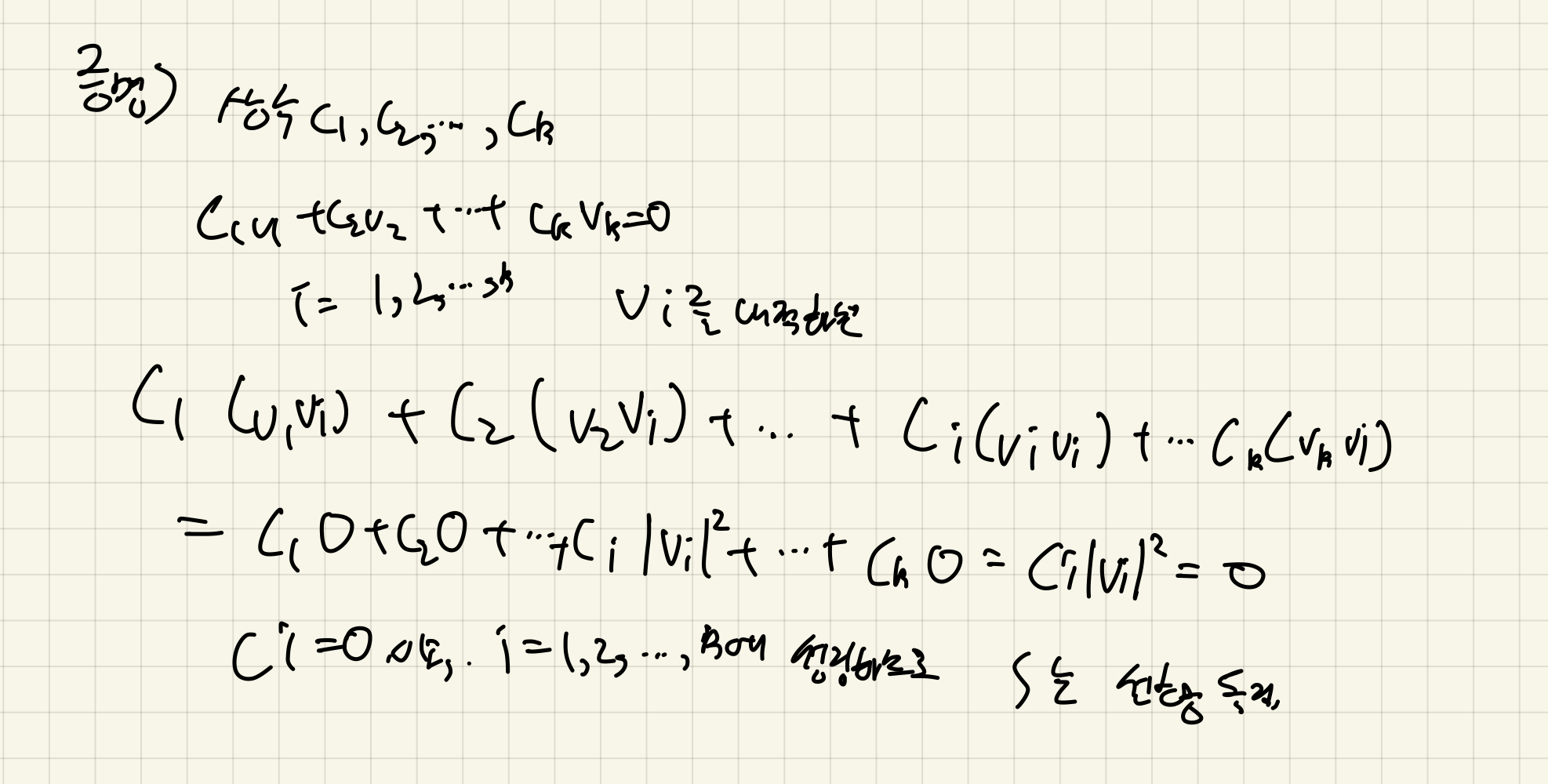
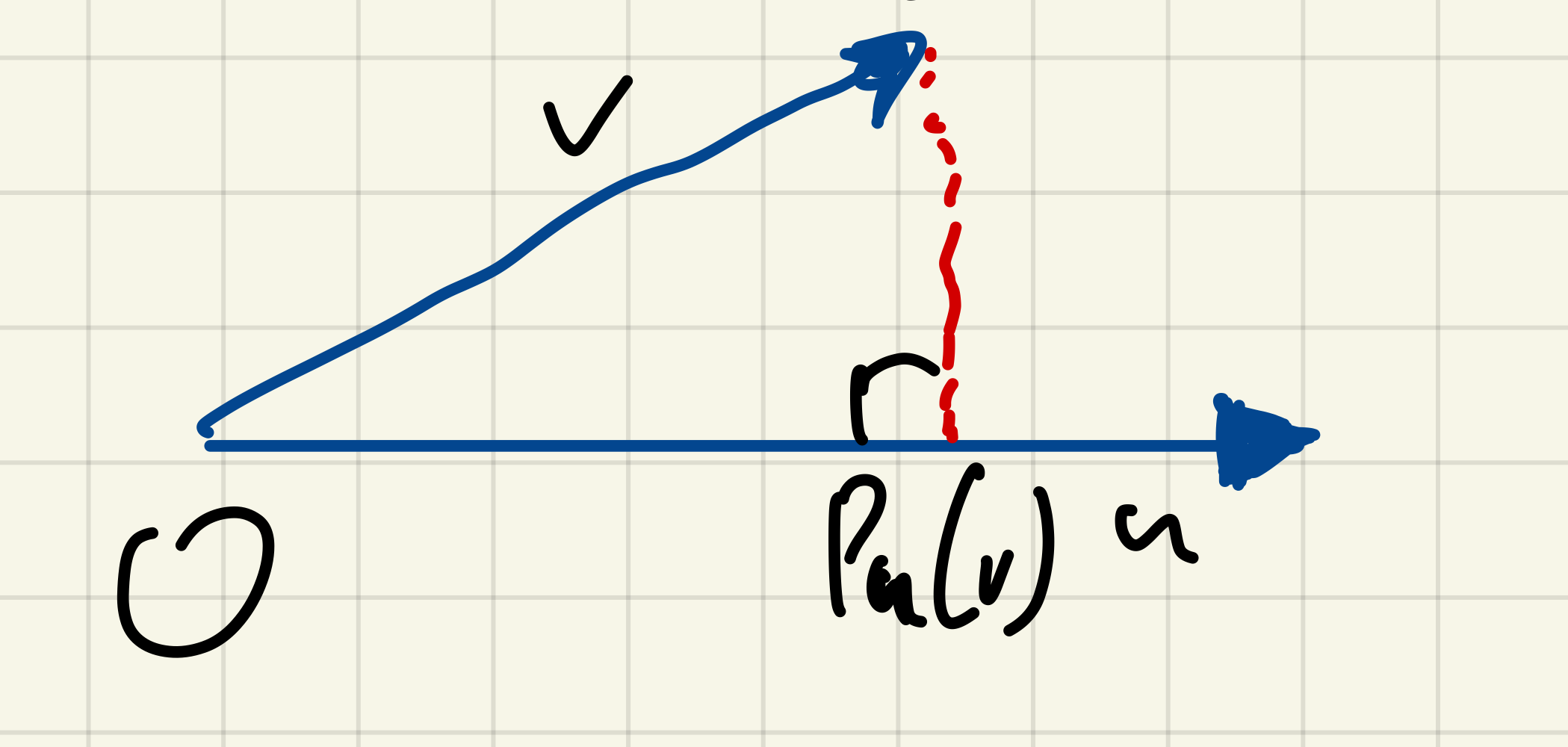
정사영
u, v != 0인 벡터에 대하여 거리가 가장 가까운 벡터를 수직으로 내린 발을 정사영이라고 한다.
코시-슈바르츠 부등식
두 개의 벡터 u, v에서 ||u·v|| <= ||u||||v||가 항상 성립한다.
증명은 아래에서 볼 수 있다.
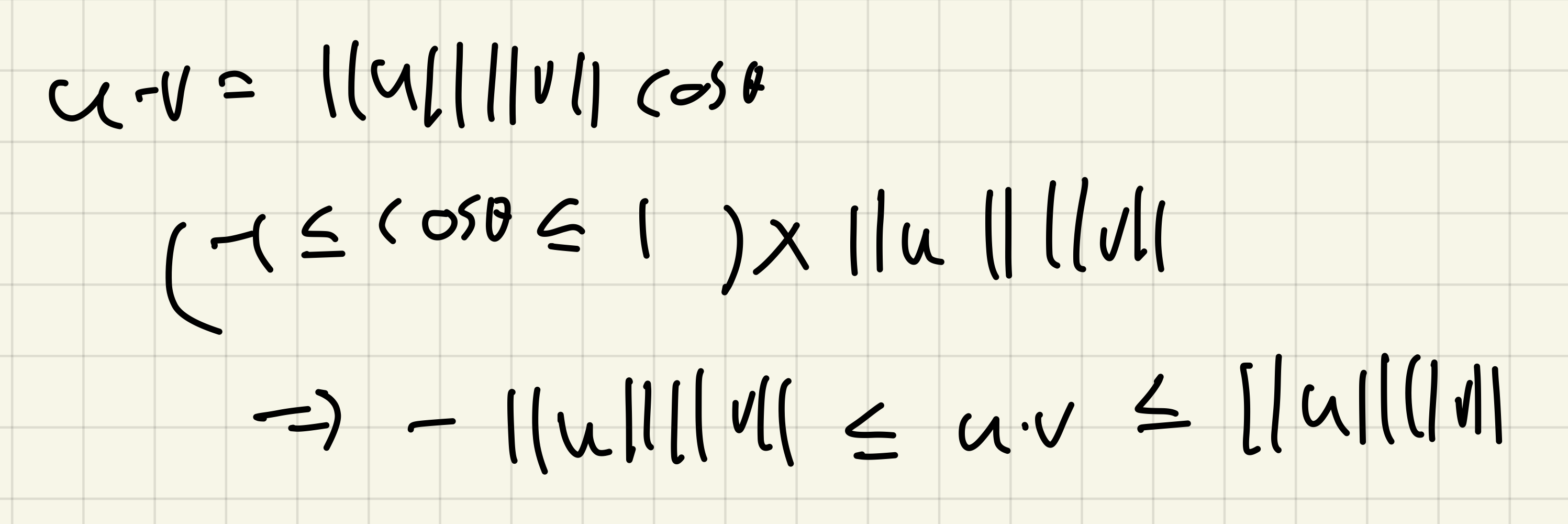
삼각 부등식
||u+v|| <= ||u|| + ||v||
가장 긴 변은 나머지 두 변의 합보다 작거나 같아야 한다.
'수학 > 선형대수' 카테고리의 다른 글
| [선형대수] 7. 선형변환 (0) | 2024.01.12 |
|---|---|
| [선형대수] 6-2. 외적 (0) | 2024.01.11 |
| [선형대수] 5-2. 생성, 기저, 차원 (0) | 2024.01.09 |
| [선형대수] 5-1. 벡터공간 (0) | 2024.01.08 |
| [선형대수] 4. 벡터 (0) | 2024.01.07 |




