Notice
250x250
Recent Posts
Recent Comments
Link
넘치게 채우기
[자료구조] 4-2. 트리의 순회(Traversal) 본문
728x90
반응형
트리의 모든 노드들을 방문하는 과정을 트리의 순회라고 한다.
스택, 큐, 연결 리스트와 같은 선형 자료구조에서는 순차적으로 노드들을 방문하지만,
비선형 자료구조인 트리에서는 다음과 같은 재귀적인 방법들이 있다:
- 전위 순회(Preorder)
- 중위 순회(Inorder)
- 후위 순회(Postorder)
전위 순회
루트 → 왼쪽 서브트리 → 오른쪽 서브트리 순으로 순회.

코드 구현
|
def preorder_traversal(self, node): #전위 순회
print(node.data, end=" ")
if node.left:
self.preorder_traversal(node.left)
if node.right:
self.preorder_traversal(node.right)
|
cs |
|
A B D E C F G
|
cs |
중위 순회
왼쪽 서브트리 → 루트 → 오른쪽 서브트리 순으로 순회.

코드 구현
|
def inorder_traversal(self, node): #중위 순회
if node.left:
self.inorder_traversal(node.left)
print(node.data, end=" ")
if node.right:
self.inorder_traversal(node.right)
|
cs |
|
D B E A F C G
|
cs |
후위 순회
왼쪽 서브트리 → 오른쪽 서브트리 → 루트 순으로 순회.
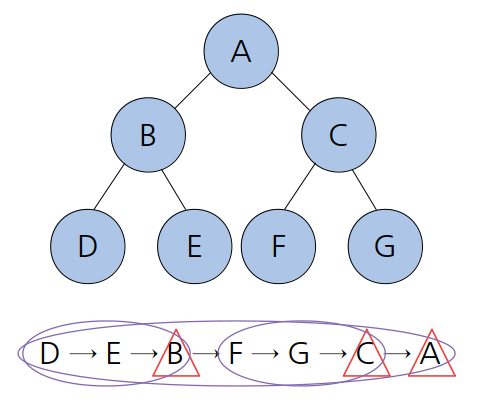
코드 구현
|
def postorder_traversal(self, node): #후위 순회
if node.left:
self.postorder_traversal(node.left)
if node.right:
self.postorder_traversal(node.right)
print(node.data, end=" ")
|
cs |
|
D E B F G C A
|
cs |
전체 코드
|
class Node(): #노드 선언
def __init__(self, data):
self.data = data
self.left = None
self.right = None
class Tree(): #트리 및 순회
def __init__(self):
self.root = None
def preorder_traversal(self, node): #전위 순회
print(node.data, end=" ")
if node.left:
self.preorder_traversal(node.left)
if node.right:
self.preorder_traversal(node.right)
def inorder_traversal(self, node): #중위 순회
if node.left:
self.inorder_traversal(node.left)
print(node.data, end=" ")
if node.right:
self.inorder_traversal(node.right)
def postorder_traversal(self, node): #후위 순회
if node.left:
self.postorder_traversal(node.left)
if node.right:
self.postorder_traversal(node.right)
print(node.data, end=" ")
|
cs |
실행
|
#트리 및 노드의 선언
T = Tree()
A = Node("A")
B = Node("B")
C = Node("C")
D = Node("D")
E = Node("E")
F = Node("F")
G = Node("G")
T.root = A
A.left = B
A.right = C
B.left = D
B.right = E
C.left = F
C.right = G
T.preorder_traversal(T.root)
print()
T.inorder_traversal(T.root)
print()
T.postorder_traversal(T.root)
|
cs |
결과
|
A B D E C F G #전위 순회
D B E A F C G #중위 순회
D E B F G C A #후위
|
cs |
728x90
반응형
'컴퓨터과학 > 자료구조' 카테고리의 다른 글
| [자료구조] 4-4. AVL 트리 (0) | 2022.12.12 |
|---|---|
| [자료구조] 4-3. 이진 탐색 트리(Binary Search Tree) (0) | 2022.12.01 |
| [자료구조] 4-1. 트리(Tree) 용어와 서브 트리, 이진트리의 개념 (0) | 2022.11.09 |
| [자료구조] 3. 해시 테이블(Hash Table) (0) | 2022.11.06 |
| [자료구조] 2-4. 덱(deque) (0) | 2022.10.26 |




