넘치게 채우기
[자료구조] 4-3. 이진 탐색 트리(Binary Search Tree) 본문
이진 탐색 트리?
이진 탐색 트리는 다음과 같은 조건이 있다:
- 같은 key값을 가지는 노드는 없다.
- 루트노드의 왼쪽 서브트리는 루트노드보다 작은 값들만 있어야 한다.
- 루트노드의 오른쪽 서브트리는 루트노드보다 큰 값들만 있어야 한다.
- 루트노드의 서브트리들 모두 이진 탐색 트리여야 한다.
이 조건들로, 이진 탐색 트리를 순회할 때 에는 보통 중위 순회를 이용한다.

이진 탐색 트리에는 세 가지 연산이 있다.
- 탐색(Search)
- 삽입(Insert)
- 삭제(Delete)
탐색
- 만약, 루트와 같은 값을 가진다면, 탐색을 멈춘다. 루트가 없는 경우 역시 탐색을 멈춘다.
- 만약, 루트보다 작은 값을 가진다면 왼쪽 서브트리에서, 더 큰 값을 가지면 오른쪽 서브트리에서 재귀한다.

구현
|
def _search(self, root, key): #탐색
if root == None: #만약 root값이 없으면: (찾지 못한 경우)
return "Not Found!"
if root.key == key: #값을 찾으면:
return root.key
elif root.key > key: #root가 더 크다면: (왼쪽으로 이동하는 재귀)
return self._search(root.left, key)
else: #root가 더 작다면: (오른쪽으로 이동하는 재귀)
return self._search(root.right, key)
|
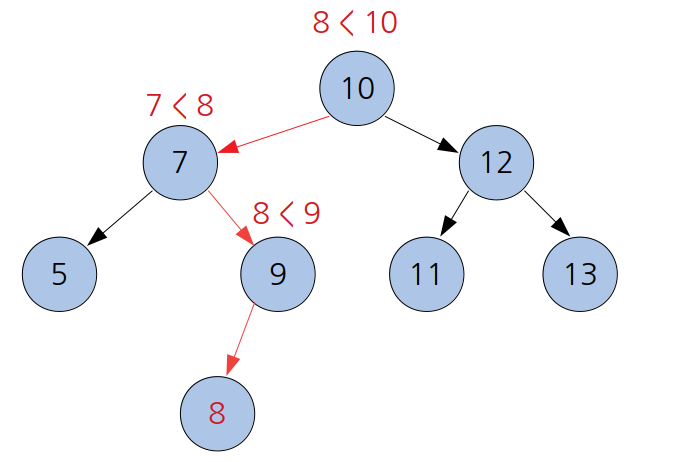
삽입
- 루트와 값이 같으면 오류가 발생된다.
- 루트보다 작으면 왼쪽 서브트리로, 크면 오른쪽 서브트리로 내려간다.
- 재귀적으로 계속 내려가다가, None인 서브트리에 넣으면 된다.
구현
|
def _insert(self, key):
def _addNode(root, key): #노드 추가 정의
if key == root.key: #루트와 같은 key라면, False반환
return False
elif key < root.key: #루트보다 작은데..
if root.left == None:#루트의 왼쪽이 비었다면? 바로 왼쪽에 삽입하면된다.
root.left = Node(key)
return True
else: #아니라면, 루트의 왼쪽 서브트리를 루트로 하고, 재귀적으로 실행시킨다.
_addNode(root.left, key)
else: #루트보다 큰데..
if root.right == None:#루트의 오른쪽이 비었다면? 바로 오른쪽에 삽입하면된다.
root.right = Node(key)
return True
else: #아니라면, 루트의 오른쪽 서브트리를 루트로 하고, 재귀적으로 실행한다.
_addNode(root.right, key)
if self.root == None: #만약 루트가 없으면, 루트부터 만들어주자
self.root = Node(key)
return True
else: #루트가 없으면? 정의해놓은 노드 추가를 이용하자.
_addNode(self.root, key)
|
삭제
삭제에는 세 가지 경우가 있다:
- 삭제하려는 노드가 잎 노드일 경우(차수가 0인 경우)
- 노드의 서브트리가 하나일 경우(차수가 1인 경우)
- 노드의 서브트리가 두 개일 경우(차수가 2인 경우)
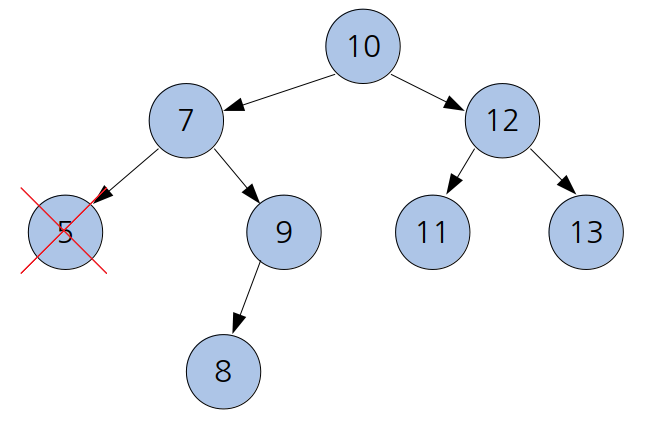
삭제하려는 노드가 잎 노드일 경우(차수가 0인 경우)
차수가 0인 경우는 간단하다. 그냥 노드를 찾아서 없애주면 된다.

구현
|
if parent.key > key: #부모노드가 더 크면, 왼쪽을 없애고, 작으면 오른쪽을 없앰
parent.left = None
else:
parent.right = None
|
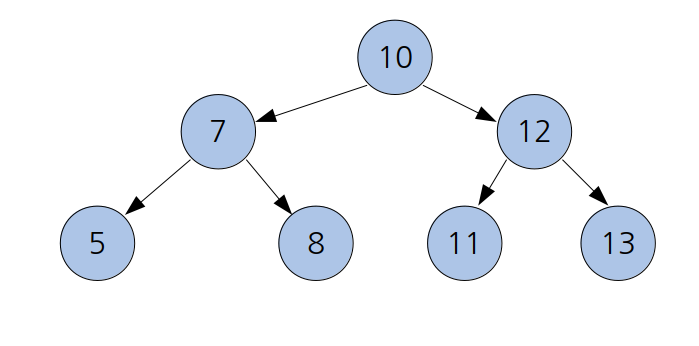
노드의 서브트리가 하나일 경우(차수가 1일 경우)
차수가 1일 경우까지도 간단하다. 없앨 노드의 부모 노드와 없앨 노드의 서브트리의 루트를 이어주면 된다.

구현
|
if node.left != None: #서브트리가 왼쪽에만 있다면
if node.key > parent.key:#삭제하려는 노드가 부모 노드보다 크면, 부모의 오른쪽을 왼쪽 서브트리의 루트로 연결
parent.right = node.left
else:
parent.left = node.left#삭제하려는 노드가 부모 노드보다 작으면, 부모의 왼쪽을 왼쪽 서브트리의 루트로 연결
elif node.right != None: #서브트리가 오른쪽에 있다면
if node.key > parent.key: #삭제하려는 노드가 부모 노드보다 크면, 부모의 오른쪽을 오른쪽 서브트리의 루트로 연결
parent.right = node.right
else:
parent.left = node.right#삭제하려는 노드가 부모 노드보다 작으면, 부모의 왼쪽을 오른쪽 서브트리의 루트로 연결
|
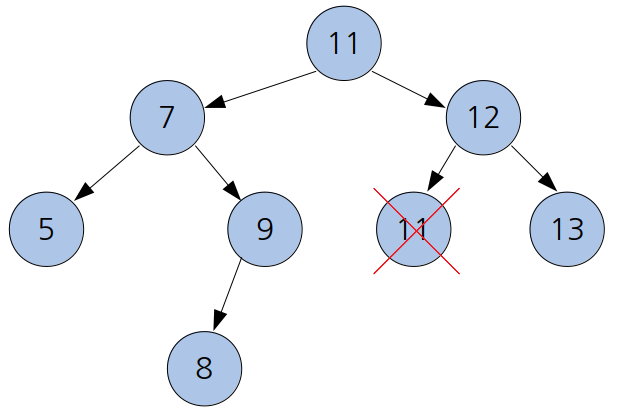
노드의 서브트리가 두 개일 경우(차수가 2일 경우) ★★★
없애는 노드의 오른쪽 서브트리의 가장 작은 자손을 없애는 노드의 자리로 대신시킨다.
또는, 왼쪽 서브트리의 가장 큰 자손으로 대신시킨다. 가장 차이가 나지 않는 값으로 바꾼다고 생각하면 된다.

구현
|
if node.left != None and node.right != None:#서브트리가 두 개일 경우,
자리를 대신할 노드로 오른쪽 서브트리의 가장 작은 자손을 올린다. minNode = node.right #오른쪽 서브트리의 루트부터 시작
parentOfmin = node #대신할 노드의 부모노드 선언
isright = True #바로 오른쪽 서브트리의 루트가 대신하는지(while 문을 건너뛰는지)
while minNode.left != None: #단말 노드까지 왼쪽으로만 내려가기
parentOfmin = minNode
minNode = minNode.left
isright = False
node.key = minNode.key #찾은 노드(오른쪽 서브트리의 가장 작은 자손)가 자리를 대신함
if isright is True: #오른쪽 서브트리의 루트가 대신한다면:
parentOfmin.right = None
else: #만약 더 내려간다면:
parentOfmin.left = None
|
전체 코드 및 실행
코드에서 구현한 트리는 위의 그림 자료와 모두 같다.
눈으로 탐색, 삽입, 삭제등의 연산을 시각적으로 보고싶다면, 다음 사이트를 이용하자: https://visualgo.net/en/bst
Binary Search Tree, AVL Tree - VisuAlgo
VisuAlgo is free of charge for Computer Science community on earth. If you like VisuAlgo, the only "payment" that we ask of you is for you to tell the existence of VisuAlgo to other Computer Science students/instructors that you know =) via Facebook/Twitte
visualgo.net
|
class Node():
def __init__(self, key):
self.key = key
self.left = None
self.right = None
class Tree():
def __init__(self):
self.root = None
def _search(self, root, key): #탐색
if root == None: #만약 root값이 없으면: (찾지 못한 경우)
return "Not Found!"
if root.key == key: #값을 찾으면:
return root.key
elif root.key > key: #root가 더 크다면: (왼쪽으로 이동하는 재귀)
return self._search(root.left, key)
else: #root가 더 작다면: (오른쪽으로 이동하는 재귀)
return self._search(root.right, key)
def _insert(self, key):
def _addNode(root, key): #노드 추가 정의
if key == root.key: #루트와 같은 key라면, False반환
return False
elif key < root.key: #루트보다 작은데..
if root.left == None:#루트의 왼쪽이 비었다면? 바로 왼쪽에 삽입하면된다.
root.left = Node(key)
return True
else: #아니라면, 루트의 왼쪽 서브트리를 루트로 하고, 재귀적으로 실행시킨다.
_addNode(root.left, key)
else: #루트보다 큰데..
if root.right == None:#루트의 오른쪽이 비었다면? 바로 오른쪽에 삽입하면된다.
root.right = Node(key)
return True
else: #아니라면, 루트의 오른쪽 서브트리를 루트로 하고, 재귀적으로 실행한다.
_addNode(root.right, key)
if self.root == None: #만약 루트가 없으면, 루트부터 만들어주자
self.root = Node(key)
return True
else: #루트가 없으면? 정의해놓은 노드 추가를 이용하자.
_addNode(self.root, key)
def _delete(self, key): #삭제
node = self.root #루트부터 시작
parent = None #없앨 부모 노드를 담을 변수 생성
while True: #무한 루프
if node == None: #노드가 없으면 중지
return False
if node.key == key:#노드의 key값이 일치하면, 루프 탈출
break
else: #같지 않으면..
parent = node
if key < node.key:#찾으려는 값이 현 노드보다 작으면, 왼쪽으로 이동해서 반복
node = node.left
else: #크면, 오른쪽으로 이동해서 반복
node = node.right
if node.left != None and node.right != None:#서브트리가 두 개일 경우, 자리를 대신할 노드로 오른쪽 서브트리의 가장 작은 자손을 올린다.
print("서브트리가 두 개!")
minNode = node.right #오른쪽 서브트리의 루트부터 시작
parentOfmin = node #대신할 노드의 부모노드 선언
isright = True #바로 오른쪽 서브트리의 루트가 대신하는지(while 문을 건너뛰는지)
while minNode.left != None: #단말 노드까지 왼쪽으로만 내려가기
parentOfmin = minNode
minNode = minNode.left
isright = False
node.key = minNode.key #찾은 노드(오른쪽 서브트리의 가장 작은 자손)가 자리를 대신함
if isright is True: #오른쪽 서브트리의 루트가 대신한다면:
parentOfmin.right = None
else: #만약 더 내려간다면:
parentOfmin.left = None
elif node.left != None: #서브트리가 왼쪽에만 있다면
print("서브트리가 한 개!")
if node.key > parent.key: #삭제하려는 노드가 부모 노드보다 크면, 부모의 오른쪽을 왼쪽 서브트리의 루트로 연결
parent.right = node.left
else:
parent.left = node.left #삭제하려는 노드가 부모 노드보다 작으면, 부모의 왼쪽을 왼쪽 서브트리의 루트로 연결
elif node.right != None: #서브트리가 오른쪽에 있다면
print("서브트리가 한 개!")
if node.key > parent.key: #삭제하려는 노드가 부모 노드보다 크면, 부모의 오른쪽을 오른쪽 서브트리의 루트로 연결
parent.right = node.right
else:
parent.left = node.right #삭제하려는 노드가 부모 노드보다 작으면, 부모의 왼쪽을 오른쪽 서브트리의 루트로 연결
else:
print("서브트리 없음!") #서브트리가 없을 때
if parent.key > key: #부모노드가 더 크면, 왼쪽을 없애고, 작으면 오른쪽을 없앰
parent.left = None
else:
parent.right = None
def inorder_traversal(self, node): #중위 순회
if node.left:
self.inorder_traversal(node.left)
print(node.key, end=" ")
if node.right:
self.inorder_traversal(node.right)
|
실행 및 결과 - 차수가 2인 노드를 없애는경우
|
BST = Tree()
BST._insert(10)
BST._insert(12)
BST._insert(13)
BST._insert(11)
BST._insert(7)
BST._insert(9)
BST._insert(8)
BST._insert(5)
print(BST._search(BST.root, 5))
BST.inorder_traversal(BST.root)
print()
BST._delete(10)
BST.inorder_traversal(BST.root)
print("이 트리의 루트는: ",BST.root.key)
print("루트의 왼쪽 서브 트리의 루트는: ", BST.root.left.key)
print("루트의 오른쪽 서브 트리의 루트는: ", BST.root.right.key)
|
|
5
5 7 8 9 10 11 12 13
서브트리가 한 개!
5 7 8 10 11 12 13 이 트리의 루트는: 10
루트의 왼쪽 서브 트리의 루트는: 7
루트의 오른쪽 서브 트리의 루트는: 12
|
실행 및 결과 - 차수가 1인 노드를 없애는경우
|
BST = Tree()
BST._insert(10)
BST._insert(12)
BST._insert(13)
BST._insert(11)
BST._insert(7)
BST._insert(9)
BST._insert(8)
BST._insert(5)
print(BST._search(BST.root, 5))
BST.inorder_traversal(BST.root)
print()
BST._delete(9)
BST.inorder_traversal(BST.root)
print("이 트리의 루트는: ",BST.root.key)
print("루트의 왼쪽 서브 트리의 루트는: ", BST.root.left.key)
print("루트의 오른쪽 서브 트리의 루트는: ", BST.root.right.key)
|
cs |
|
5
5 7 8 9 10 11 12 13
서브트리가 한 개!
5 7 8 10 11 12 13 이 트리의 루트는: 10
루트의 왼쪽 서브 트리의 루트는: 7
루트의 오른쪽 서브 트리의 루트는: 12
|
cs |
실행 및 결과 - 차수가 0인 노드를 없애는경우
|
BST = Tree()
BST._insert(10)
BST._insert(12)
BST._insert(13)
BST._insert(11)
BST._insert(7)
BST._insert(9)
BST._insert(8)
BST._insert(5)
print(BST._search(BST.root, 5))
BST.inorder_traversal(BST.root)
print()
BST._delete(5)
BST.inorder_traversal(BST.root)
print("이 트리의 루트는: ",BST.root.key)
print("루트의 왼쪽 서브 트리의 루트는: ", BST.root.left.key)
print("루트의 오른쪽 서브 트리의 루트는: ", BST.root.right.key)
|
cs |
|
5
5 7 8 9 10 11 12 13
서브트리 없음!
7 8 9 10 11 12 13 이 트리의 루트는: 10
루트의 왼쪽 서브 트리의 루트는: 7
루트의 오른쪽 서브 트리의 루트는: 12
|
cs |
이진 탐색 트리의 시간복잡도
이진 탐색 트리의 시간복잡도는 트리가 균형이 잡혀있을수록 효율적이다.
왼쪽같이 불균형한 트리는 탐색, 삽입, 삭제 모두 O(n)이 걸리고, 완전 이진 트리의 모양은 가지면, O(logN)만큼만 걸린다.

'컴퓨터과학 > 자료구조' 카테고리의 다른 글
| [자료구조] 4-5. 레드-블랙 트리(Red Black Tree) (0) | 2023.02.23 |
|---|---|
| [자료구조] 4-4. AVL 트리 (0) | 2022.12.12 |
| [자료구조] 4-2. 트리의 순회(Traversal) (0) | 2022.11.14 |
| [자료구조] 4-1. 트리(Tree) 용어와 서브 트리, 이진트리의 개념 (0) | 2022.11.09 |
| [자료구조] 3. 해시 테이블(Hash Table) (0) | 2022.11.06 |




