넘치게 채우기
[자료구조] 4-1. 트리(Tree) 용어와 서브 트리, 이진트리의 개념 본문
트리는 계층적 관계를 표현하는 자료 구조이다.
뿌리에서 가지를 늘려가며 뻗어가는 모양을 그리는 완전 그래프여서 트리라고 부른다.
회사의 조직도나, 컴퓨터 폴더의 구조에서 트리를 볼 수 있다.
용어 정리

·노드 node
트리의 구성요소가 되는 정점(A, B, C, D, E, F)
·간선 edge
노드와 노드를 연결하는 연결선
·루트 root
트리의 최상위 노드(A). 나무의 뿌리와 같은 위치에 있어서 이름이 루트이다.
·단말 노드 terminal node
아래로 또 다른 노드가 연결되어있지 않은 노드이다. 나무의 구조상 잎의 위치여서 잎사귀 노드(leaf node)라고도 한다.
·내부 노드 internal node
단말 노드를 제외한 모든 노드, 비단말 노드(nonterminal node)라고 한다.
·부모 노드 parent node
자식 노드의 상위 노드(B, C, D의 부모 노드는 A)
·자식 노드 child node
부모 노드의 하위 노드(A의 자식노드는 B, C, D)
·형제 노드 sibling node
부모가 같은 노드(B, C, D는 같은 부모를 가졌으므로 A이다.)
·조상 노드 ancestor node
특정 노드의 상위에 있는 모든 노드(E의 조상노드는 A, B)
·후손 노드 descentent node
특정 노드의 하위에 있는 모든 노드(A희 후손은 B, C, D, E, F)
·레벨 level
루트부터 시작해서 트리의 각 층마다 숫자(단계)가 하나씩 올라간다. 루트는 0
·높이 heigh
트리의 최고 높이를 말한다.
·차수 degree
노드가 가진 자식의 수
서브 트리 (Sub Tree)
큰 트리에 속하는 작은 트리를 서브트리라고 한다.

2와 3은 1의 서브트리이고,
2의 서브트리는 4와 5가 있다.
이진 트리 (Binary Tree)
이진트리는 모든 노드의 차수가 2 이하인 트리이다.
이진트리는 루트 중심으로 두 개의 서브트리로 나뉘고, 나눠진 두 개의 서브트리 모두 이진 트리이다.
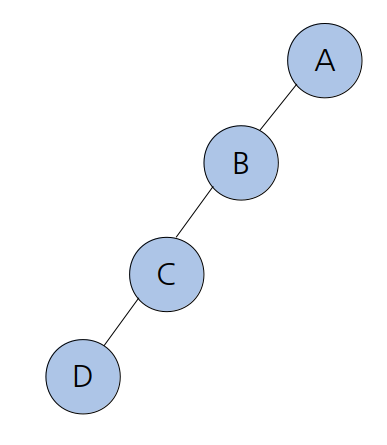
위 트리를 보자. 두 개의 서브트리로 나뉘어야 하는데, 한쪽으로만 편향되어 있는 트리이다.
놀랍게도, 이 트리는 편향 이진 트리(skewed binary tree)로, 이진트리의 일종이다.
최소 노드의 개수로 높을 레벨을 가질 수 있다.
이진트리같이 보이지는 않지만. 아래처럼 표현하면 이진트리처럼 생겼을 것이다.

노드가 위치할 수 있는 곳에 노드가 없으면, 그 자리에 공집합 노드가 존재한다. 그리고 이진 트리인지를 판별할 때 인정된다.
이 공집합 노드의 존재로, 꼭 모든 노드의 차수가 2가 아니더라도, 0이나 1이더라도 이진 트리로 볼 수 있다.
포화 이진 트리
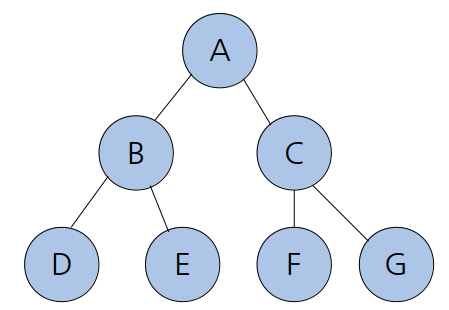
더 이상의 노드 추가는 안되고, 레벨을 늘려야 노드를 더할 수 있을 것 같다.
이렇게 모든 레벨이 꽉 찬 이진 트리를 포화 이진 트리라고 한다.
완전 이진 트리

모든 레벨이 다 찬건 아니다. 그러나, 차곡차곡 빈 틈이 없는 트리를 '완전 이진트리'라고 한다.
(차곡차곡은 노드가 위에서 아래, 왼쪽에서 오른쪽 순으로 채워진 걸 말한다.)
'컴퓨터과학 > 자료구조' 카테고리의 다른 글
| [자료구조] 4-3. 이진 탐색 트리(Binary Search Tree) (0) | 2022.12.01 |
|---|---|
| [자료구조] 4-2. 트리의 순회(Traversal) (0) | 2022.11.14 |
| [자료구조] 3. 해시 테이블(Hash Table) (0) | 2022.11.06 |
| [자료구조] 2-4. 덱(deque) (0) | 2022.10.26 |
| [자료구조] 2-3. 원형 큐 (Circular queue) (0) | 2022.10.24 |




