넘치게 채우기
[자료구조] 3. 해시 테이블(Hash Table) 본문
해시 테이블(Hash Table)은 해시 함수를 통해서 얻은 인덱스에 key 와 value값을 저장하는 자료 구조이다.
해시 함수는 같은 key값을 받으면 같은 인덱스값으로 반환시킨다.

해시 함수
해싱을 하는 해시 함수에는 다음과 같은 것들이 있다:
1. Division Method: 가장 쉽고 간단한 방법이다. key값을 해시 테이블의 크기로 나눈 나머지를 인덱스로 정하는 것이다.
h(k) = k mod m (k = key, m = size of hash table) m값은 소수이고, 2의 제곱수와 먼 값을 사용해야 효율적이라고 한다.
2. Multiplication Method: key값과 A(0 < A < 1)의 곱의 소수 부분에 테이블의 크기 m을 곱한 값의 정수값을 인덱스로 한다.
h(k) = floor(m(k*A mod 1)) (k = key, m = size of hash table, 0 < A < 1) m값이 2의 제곱수일때 제일 효율적이라고 한다.
3. Digit Folding: key의 문자열 자리마다 ASCII 코드로 바꿔서, 모든 값을 합하여 인덱스를 구한다. Division Method와 함께 사용하여 값이 과하게 커짐을 방지 할 수 있다.
h(k) = (k1 + k2 + k3 + ... + kn) mod m (n글자짜리 key가 입력되었다고 가정하였을 때)
해시 충돌(Collision)
해시 테이블에 데이터를 넣다 보면, 다음과 같은 경우들이 생긴다:
1. 해시 함수가 다른 key값을 받았지만 같은 인덱스를 배정해주었을 때
2. 적재율(n/m, n = 키의 개수, m = 테이블의 크기)이 1을 넘어 비둘기집의 원리로 인해 어느 인덱스에서 두 개의 key가 들어왔을 때
이와 같이 동일 인덱스에 매핑된 경우를 해시 충돌이라고 한다. 해결책은 크게 두 가지가 있다.
분리 연결법(Seperate Chaining)

closed addressing이라고도 하는 체이닝은 무슨 일이 있어도 이 슬롯에 넣겠다는 의미를 가지고 있다.
연결 리스트를 활용하여 같은 인덱스에 왔으나, 뒤로 계속 데이터를 이어나갈 수 있다. 이러면 적재율에 대한 걱정도 할 필요없다.
그러나, 추가 메모리를 계속 사용하게 되고, 테이블의 빈 공간이 계속 있는데도, 한 곳에만 계속 쌓일 수 있어서 최악의 경우,
찾고싶은 데이터를 찾으려면 O(n)이 걸릴 수도 있다.
Open Addressing
오픈 어드레싱은 충돌이 발생하였을 때, 다른 빈 슬롯을 찾아 넣는 방법을 말한다. 아래 세 가지의 종류가 있다.
선형 조사법(linear Probing)
만약 해싱된 값h(k) 인덱스에 이미 데이터가 있다면, h(k)+1, h(k)+2 , ... 등 인덱스를 하나씩 늘려가면서 빈 버킷이 없는지 탐색한다. 최대 값을 넘으면, 인덱스 0부터 시작한다. 빈 버킷을 찾으면 그 공간에 데이터를 저장하면서 마무리한다.

Linear Probing으로 채워진 슬롯들이 많아질수록, 다음에 탐색할 양이 더 늘어날 수 있기 때문에 비효율적일 수 있다.
연속되게 채워진 것을 primary cluster라고 하는데, 이 값이 생기면 점점 더 커지고, 탐색 시간은 이 값에 비례하기된다.
클러스터가 커지면 충돌 지점이 몰리는 것이다. 충돌 지점이 몰리면 결국 충돌이 늘어날 수 밖에 없다.
이 단점을 보완하기 위해서 Quadratic Probing이 생겼다.
이차 조사법(Quadratic Probing)
충돌이 발생할 때 마다, h(k) + 1^2, h(k) + 2^2, ... h(k) + n^2인덱스에 데이터 삽입을 시도한다.
더 먼곳에서 빈칸을 찾아서, 다음 충돌의 확률을 줄여준다.
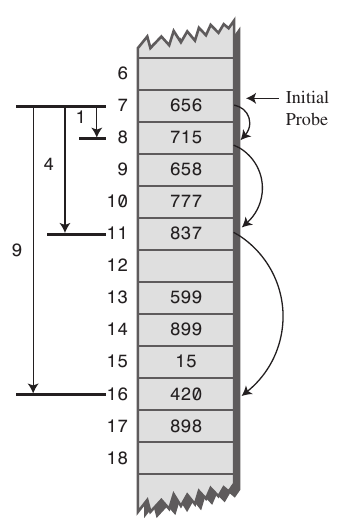
이 방법은 일정한 인덱스에 값이 몰리는 현상을 방지한다. 그러나, 중간에 빈 공간들이 많이 생기게 된다.
그리고, 결국 새로운 곳에 새로운 클러스터가 생겨 좋지 못한 분포가 생기게 된다. 이를 secondary clustering이라고 한다.
슬롯의 삭제
선형, 이차 조사법으로 충돌을 해결할 때, 슬롯의 데이터 삭제를 빈 공간으로 두는 것이 아닌, 따로 표시를 해두어야 한다.

위 그림은 Division Method를 이용하는 a%7 해시 함수를 쓰는 해시 테이블이고, 처음에 9를 넣었다가, 2를 넣고, 선형 조사법으로 2가 [3]에 들어간 상황이다.
이제, 테이블에 2가 있는지를 찾으려 하는데, 만약 [2]가 똑같이 빈칸으로 저장되면 어떻겠는가? [2]가 빈칸임을 보고 탐색을 멈출 것이다. [3]에 있는데도 말이다.
그러나, [Deleted]로 현재는 빈칸이나, 이전에 데이터가 있었다고 표시하면, 조사법으로 다른 슬롯들도 찾아보았을 것이다.
Deleted로 저장함으로써, 충돌로 인한 문제들 중 하나를 해결해줄 수 있다.
이중 해시(Double Hash)
이차 조사법도 결국에는 같은 해시를 가지면, 규칙적인 값이 더해져서 같은 위치로 옮기기 때문에 충돌이 일어나게 된다.
이 한계를 극복하기 위해서, 빈 공간으로 가는 값을 불규칙적으로 바꾸는 이중 해시가 있다.
충돌이 발생할 때, 2차 해싱을 이용한다.
step = C - k mod C = 1 + k mod C (C는 보통 테이블의 크기 m보다 작은 소수이다)
1을 더하는 이유는 2차 해시 값이 0이 되는 걸 막기 위해서이다. 테이블의 크기보다 작은 소수로 결정하는 이유는, 2차 해시 값이
1차 해시값을 넘지 않게 하기 위해서이다. 원래 해시 값보다 점프해야 하는 값이 더 크면 비효율적이고 이상하지 않은가?
그리고, C의 값을 소수로 정하였을 때, 클러스터의 발생이 낮아진다는 통계가 있다고 한다.
이 함수는 1 ~ C의 값을 반환하고, 충돌이 생기면, h(k) + 1*step, h(k) + 2*step , ...을 조사하고, 빈 공간이면 조사를 멈춘다.
이중 해싱은 한곳에 값이 몰리는 것을 방지한다. 같은 버켓을 사용하더라도, 같은 step까지 가지기는 힘들기 때문이다.
띄우는 간격이 서로 달라, 클러스터의 크기를 최소화 시켜서 가장 이상적인 Open Addressing을 할 수 있다.
코드 구현(Chaining 이용)
|
class hashTable():
def __init__(self, size):
self.size = size
self.table = [None for _ in range(self.size)]
def _func(self, key): #해시 함수
a = 0
for i in range(len(key)):
a = ord(key[i])
return a % self.size
def _add(self, key, value): #해시 함수에 값 추가. 같은 슬롯에 값이 있으면, 그 뒤에 연결한다.
idx = self._func(key)
if self.table[idx] == None:
self.table[idx] = [[key, value]]
else:
self.table[idx].append([key, value])
def _del(self, key): #해시 함수에서 해당 key를 가진 값 제거.
idx = self._func(key)
if self.table[idx] == None: #일단 해싱된 값이 비면 없다는 뜻이고,
print("No data", key ,"!")
else:
for i in range(len(self.table[idx])):
if self.table[idx][i][0] == key:
self.table[idx].pop(i)
return
print("No data", key ,"!") #탐색하고 나서 없을때도 없다고 출력한다.
def _printAll(self): #해시 함수 전체 출력
for i in range(self.size):
print(self.table[i])
def _search(self, key): #탐색. 제거하는 함수와 비슷하다.
idx = self._func(key)
if self.table[idx] == None:
print("No data", key ,"!")
else:
for i in range(len(self.table[idx])):
if self.table[idx][i][0] == key:
print(self.table[idx][i][1])
return
print("No data", key ,"!")
|
cs |
실행 예제
|
a = hashTable(5)
a._add('서울', '02')
a._add('경기', '031')
a._add('인천', '032')
a._printAll()
print("///")
a._del('부산')
a._search('경기')
print("///")
a._del('서울')
a._printAll()
|
cs |
|
[['인천', '032']]
None
[['서울', '02'], ['경기', '031']]
None
None
///
No data 부산 !
031
///
[['인천', '032']]
None
[['경기', '031']]
None
None
|
cs |
'컴퓨터과학 > 자료구조' 카테고리의 다른 글
| [자료구조] 4-2. 트리의 순회(Traversal) (0) | 2022.11.14 |
|---|---|
| [자료구조] 4-1. 트리(Tree) 용어와 서브 트리, 이진트리의 개념 (0) | 2022.11.09 |
| [자료구조] 2-4. 덱(deque) (0) | 2022.10.26 |
| [자료구조] 2-3. 원형 큐 (Circular queue) (0) | 2022.10.24 |
| [자료구조] 2-2. 큐(Queue) (0) | 2022.10.13 |




