넘치게 채우기
[자료구조] 4-10. B-트리 본문
B-트리
B-트리는 스스로 균형을 맞추는 자가 균형 이진 트리의 확장판이다. 기존 이진 트리와 다른 점은, 한 노드에서 여러 개의 데이터를 가진다는 점이다.
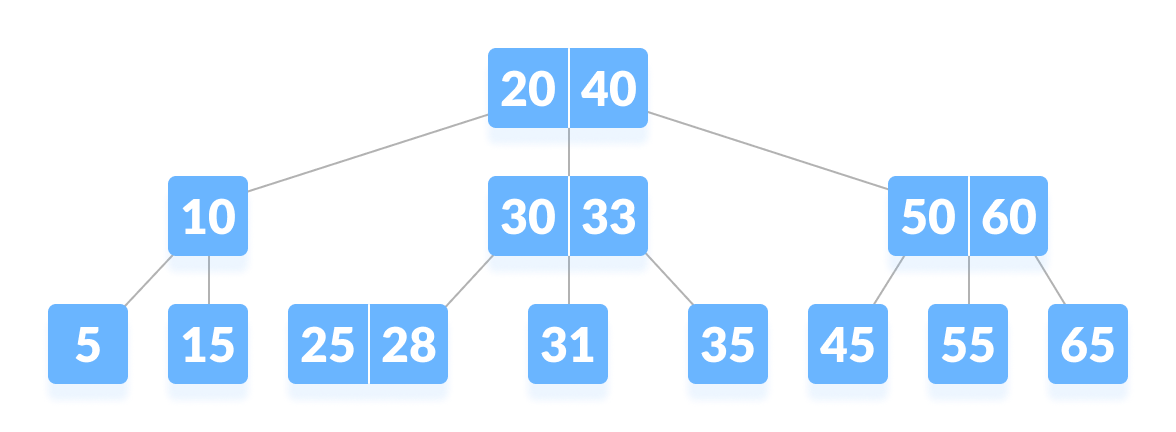
B트리는 탐색, 삽입, 삭제 모두 O(log N)의 시간복잡도를 가진다.
주로 디스크와 같은 물리저장소에서 빠르게 접근하기 위해서 사용된다.
B트리는 다음과 같은 특징을 가진다:
1. 노드의 key 수가 k개이면, 노드의 자식은 k+1개여야 한다.
2. 노드의 key는 정렬되어야 한다.
3. 자식 노드의 key는 현재 노드의 key를 기준으로 나뉜다.
4. root 노드는 2개 이상의 자식노드를 가진다.(단, root 노드가 leaf인 경우에는 제외)\
5. M차 트리일 때, 노드가 가질 수 있는 key값은 floor(M/2)-1부터 M-1개까지 가질 수 있다(floor = 소수점 버림 = 3.5 ->3)
내부 노드(root와 leaf를 제외한 노드)는 최소 M/2개부터 최대 M개의 서브트리를 가진다.
6. 모든 leaf 노드는 같은 층에 있다.
B트리의 탐색
B트리의 탐색 과정은 다음과 같다:
1. 루트 노드부터 시작한다.
2. 현재 노드의 가장 작은 key부터 값을 찾는다.
3. 찾는 값이 노드 안에 있다면 탐색을 마치고, 찾는 값보다 더 큰 key를 마주치면 그 key의 바로 왼쪽 자식 노드로 이동한다.
마지막 key 값보다 크면, 그 key의 오른쪽 자식 노드로 간다.
4. 2~3과정을 반복한다.
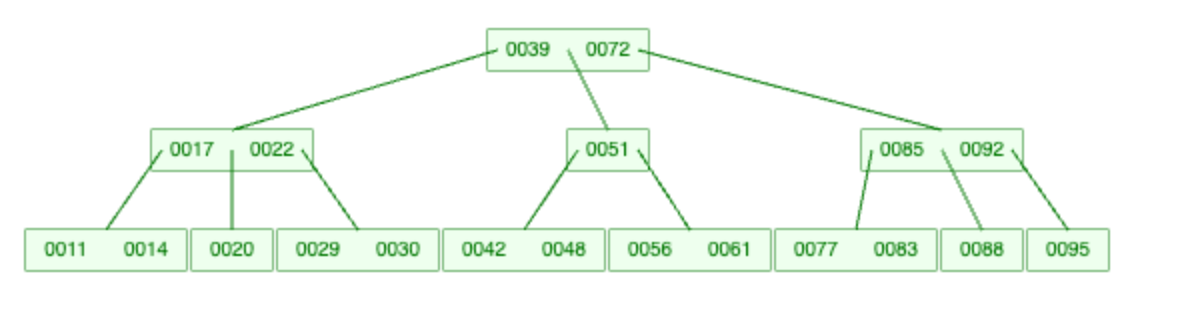
위 트리에서 20을 탐색한다고 할 때,
20 < 39 이므로 39의 왼쪽 자식 노드로 내려간다. -> 20 > 17 이므로 다음 key와 비교한다. 20 < 17 이므로 22의 왼쪽 자식 노드로 이동한다. -> 20을 발견하고 탐색을 마친다.
B트리의 삽입
B트리의 삽입 과정은 다음과 같다:
1. 루트 자리가 비어있다면, 노드를 하나 삽입하고, 루트로 지정한다.
2. 비어 있지 않다면, 데이터를 넣을 리프 노드를 탐색하고, 탐색과 똑같은 과정을 밟은 뒤, 리프 노드의 적절한 자리에 key를 넣는다.
3. 삽입된 노드의 조건이 깨지면(노드에 key가 M개 이상 있다면): 노드를 분리한다. 노드의 가운데 값이 부모로 올라가고, 그의 왼쪽 key는 왼쪽자식, 오른쪽 key는 오른쪽 자식으로 한다.
아래는 3차 B트리에서 17을 삽입하는 과정이다.

B트리의 삭제
B트리의 삭제과정은 다음과 같다:
Case 1. 리프 노드를 삭제하는 경우
1-1. 노드를 삭제해도 조건을 만족하는 경우: 노드를 삭제하고 끝낸다.
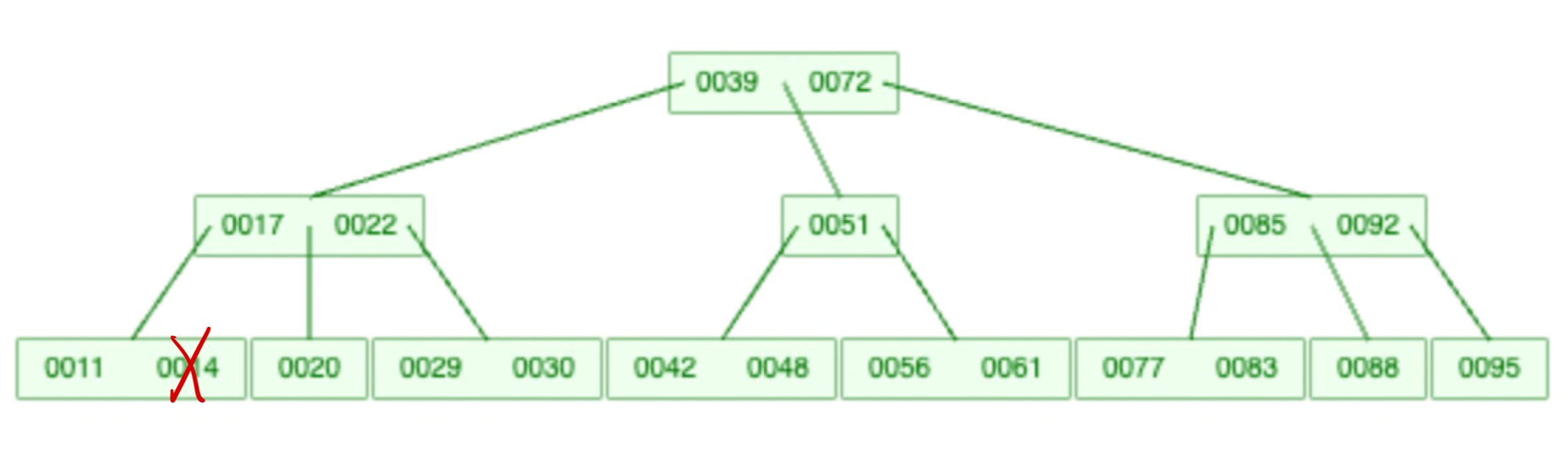
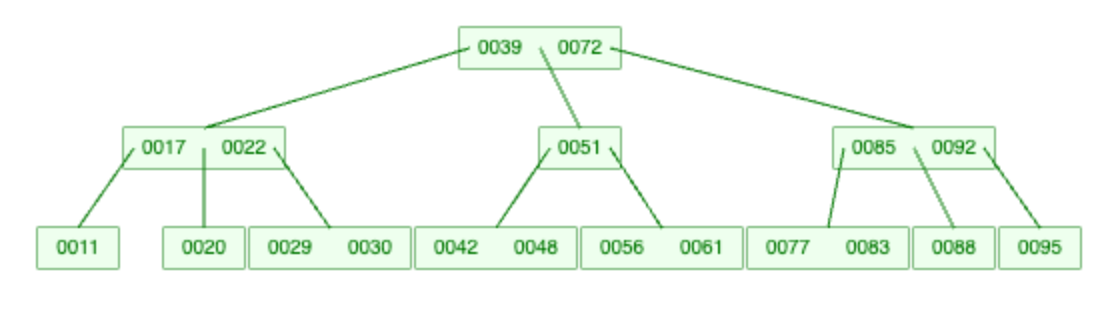
1-2. 조건이 깨지지만 바로 옆형제가 해결해주는 경우:
노드가 삭제되는 자리에 부모 노드가 내려가고, 그 부모 노드자리를 바로 옆의 형제노드가 해결해준다.
왼쪽 형제에게 빌리는 경우, 왼쪽 노드의 가장 큰 값이 부모노드를 대신한다.
오른쪽 형제에게 빌리는 경우, 오른쪽 노드의 가장 작은 값이 부모노드를 대신한다.


1-3. 바로 옆형제에게 빌릴 수 없고, 부모노드에서 분할 가능한 경우:
노드를 삭제하고, 부모 노드를 분할해서 옆의 형제 노드의 붙인다.(리프를 없애면서 부모노드의 key수도 같이 줄이는 방법)
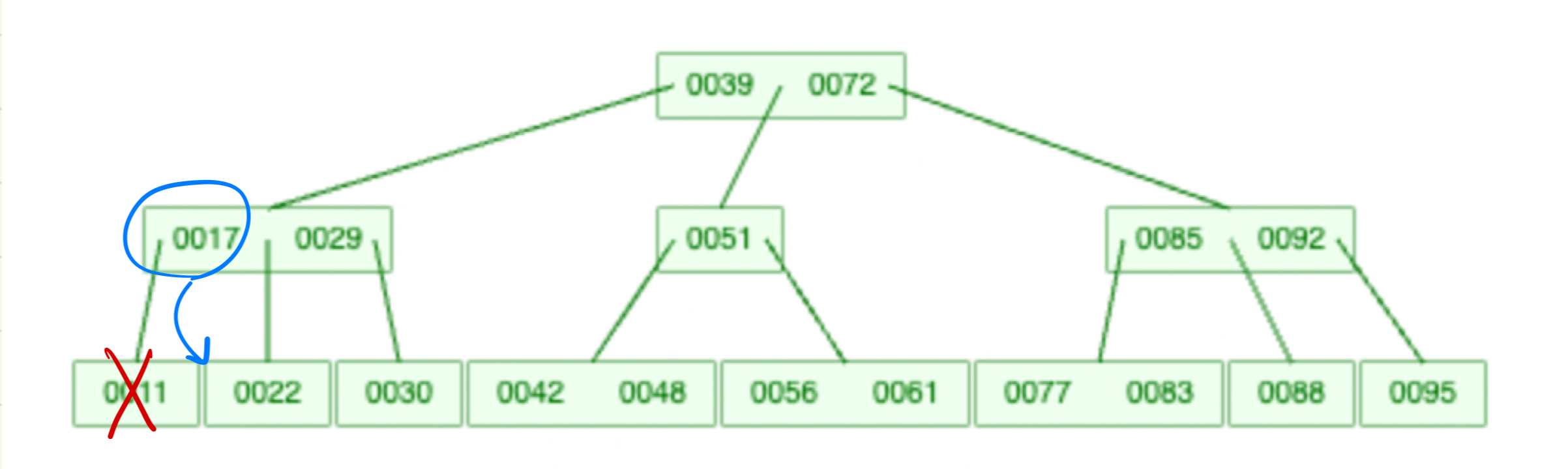
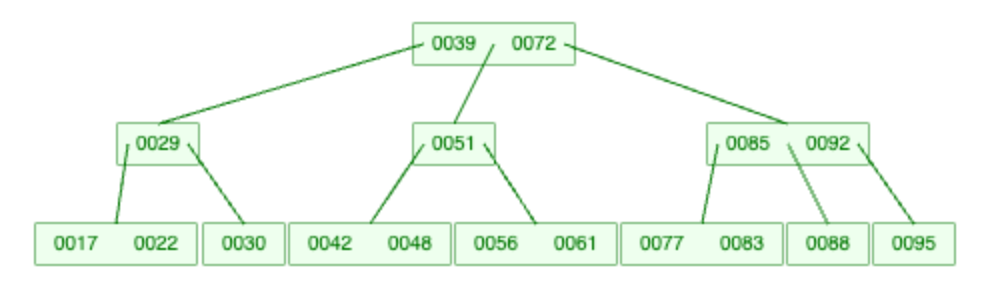
Case 2. Leaf가 아닌 노드의 삭제
2-1. leaf의 key의 수가 최소보다 많은 경우: Leaf 노드에서 자신을 대체할 수 있는 key를 찾아서 자리에 놓는다.
(왼쪽서브트리의 최대 또는 오른쪽서브트리의 최소) 그뒤, 그 리프노드의 key를 제거한다.
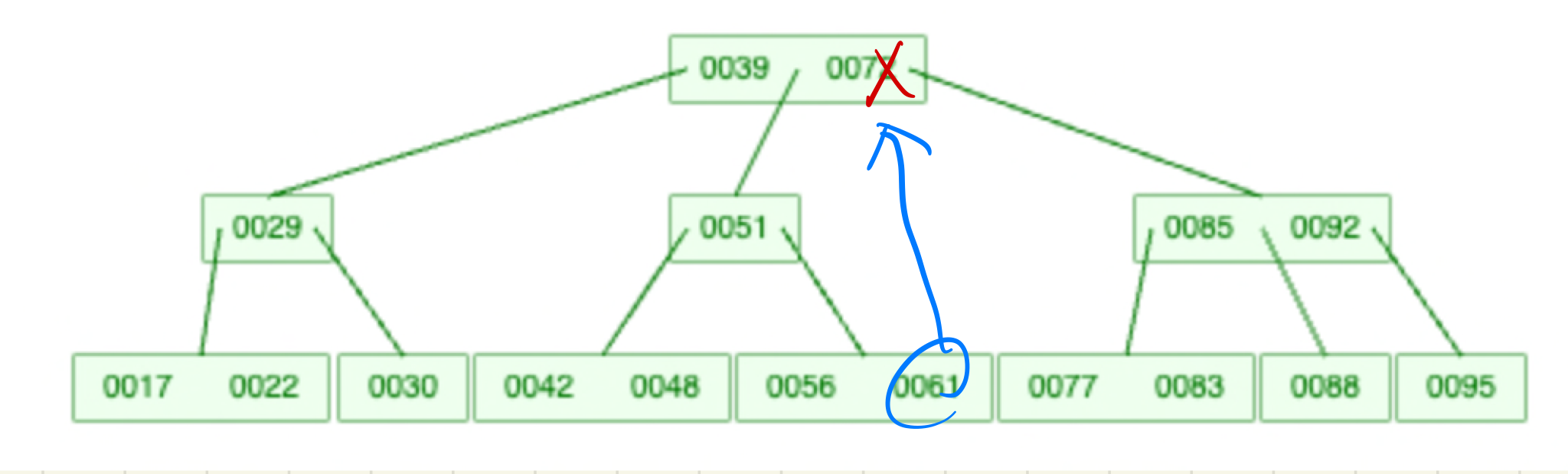

2-2. 자신이 최소 key의 수보다 많으나, 자식들은 그렇지 못한경우:
두 자식을 병합시킨다.
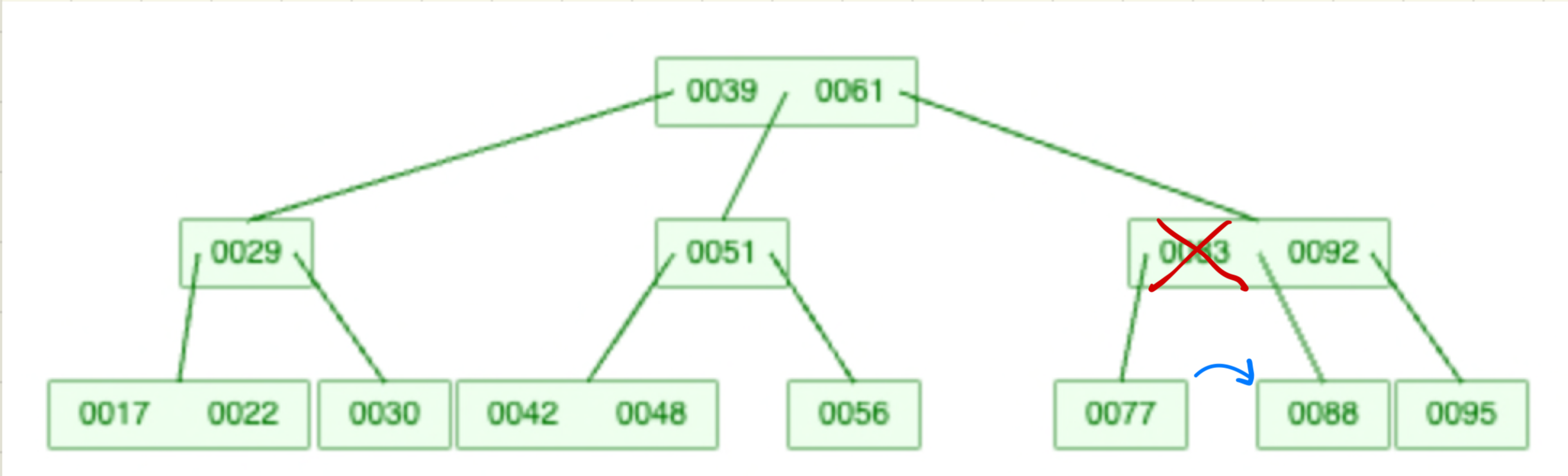

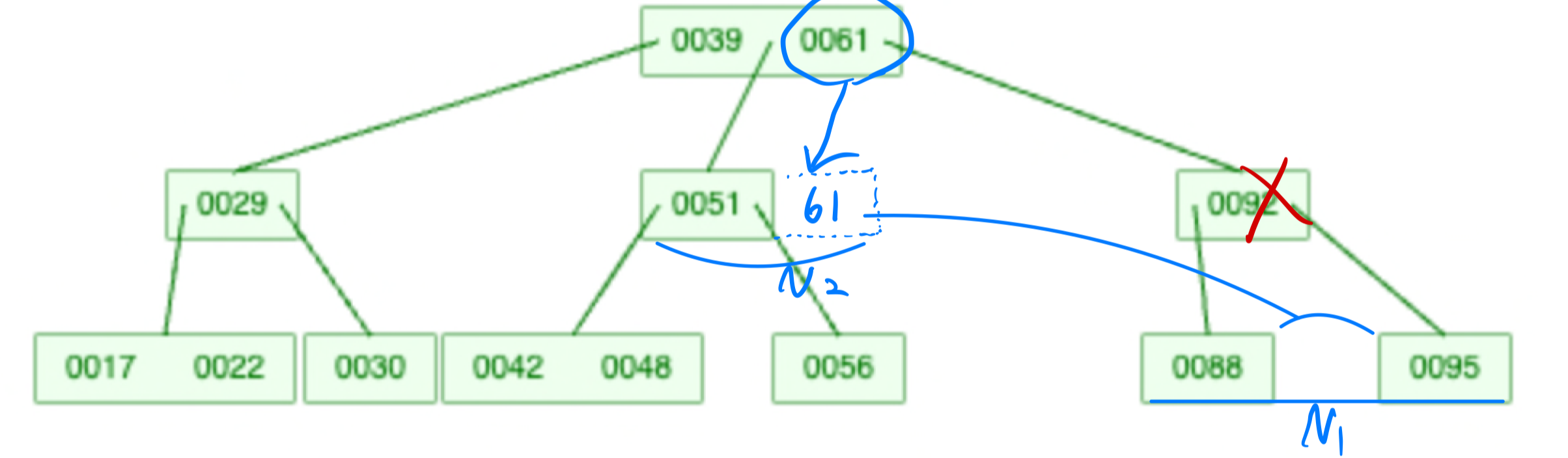
2-3. 자신과 자식들 모두 최소한의 key만 가진경우:
부모노드를 내려서 형제노드에 붙이고 -> 노드 N2
자식노드들을 합친다 -> 노드 N1
N1을 N2의 자식으로 연결한다.

'컴퓨터과학 > 자료구조' 카테고리의 다른 글
| [자료구조] 5. 그래프 이론(Graph Theory) (0) | 2023.04.16 |
|---|---|
| [자료구조] 4-11. B+트리와 B*트리, 2-3-4 트리 (0) | 2023.04.16 |
| [자료구조] 4-9. 힙(Heap)과 우선 순위 큐(Priority Queue) (0) | 2023.04.14 |
| [자료구조] 4-8. 트라이(Trie) (0) | 2023.04.14 |
| [자료구조] 4-7. 레드-블랙 트리의 삭제(Deletion in Red-Black Tree) (0) | 2023.04.12 |




