넘치게 채우기
[자료구조] 4-7. 레드-블랙 트리의 삭제(Deletion in Red-Black Tree) 본문
레드블랙트리의 삭제의 순서는 다음과 같다:
1. 삭제할 노드를 찾는다
2. 삭제할 노드의 자식이
a. 둘인 경우 - 없앨 노드의 오른쪽 서브트리의 가장 왼쪽 노드(또는 왼쪽 서브트리의 가장 오른쪽 노드)로 노드를 바꾸고, 그 잎 노드를 없애준다.
b. 하나인 경우 - 삭제되는 노드의 부모노드와 자식노드를 연결시킨다.
c. 없는 경우 - 노드를 없애주면 된다.
여기까지는 이진탐색트리의 노드제거와 같다.
3. 삭제되는 노드의 색깔이 빨간색인 경우, 여전히 레드블랙트리의 규칙을 만족하므로 삭제가 완료된다.
그러나, 삭제되는 노드의 색이 검은색인 경우, 그 자리를 대체하는 노드를 검은색으로 칠한다.
여기서, 대체하는 노드 역시 검은색인 경우, 이중 흑색노드가 생긴다.
그럼, 이중 흑색노드를 어떻게 해결하냐?
Case 0. 이중 흑색노드의 형제가 빨간색인 경우

이중흑색노드의 형제의 색을 검은색, 부모의 색을 빨간색으로 칠해준다. 그 다음, 이중흑색노드의 방향으로 회전시킨다.
(이중흑색노드가 왼쪽자식이면 좌회전, 오른쪽자식이면 우회전)
그 뒤, 상황에 맞게 아래 1~3번의 케이스로 넘어간다.
Case 1. 이중 흑색노드의 형제가 검은색, 형제의 양쪽 자식 모두 검은색인 경우
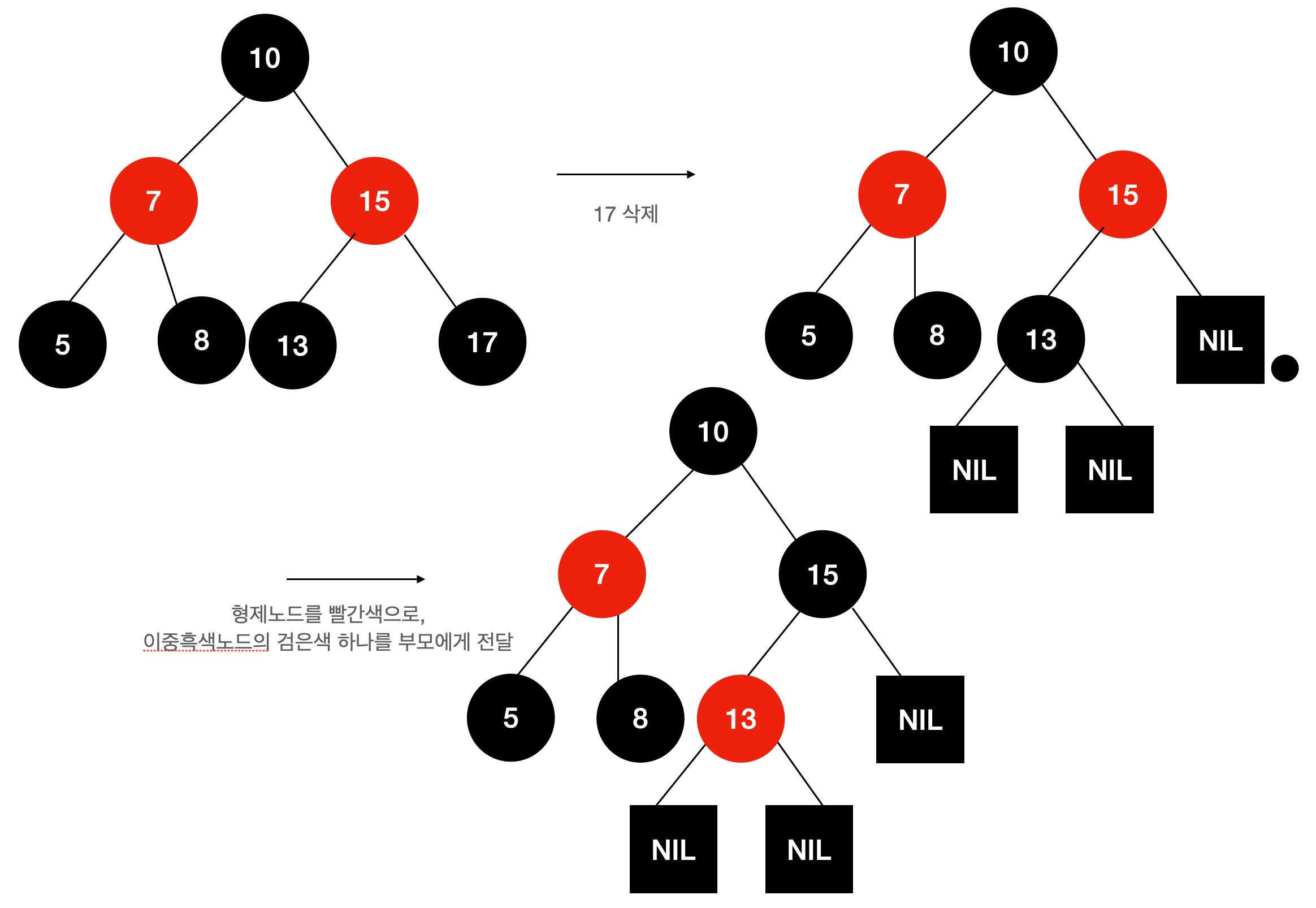
형제 노드의 색을 레드로 만들고, 이중흑색노드의 검은색 하나를 부모 노드에게 넘긴다. 부모 노드와 두 자식노드가 리컬러링된다고 생각하면 된다.(이중 흑색노드는 빨간색이 되는 대신 검은색 하나를 잃는다)
Case 2. 이중 흑색노드의 형제가 검은색, 형제의 왼쪽 자식이 빨간색, 오른쪽 자식이 검은색인 경우
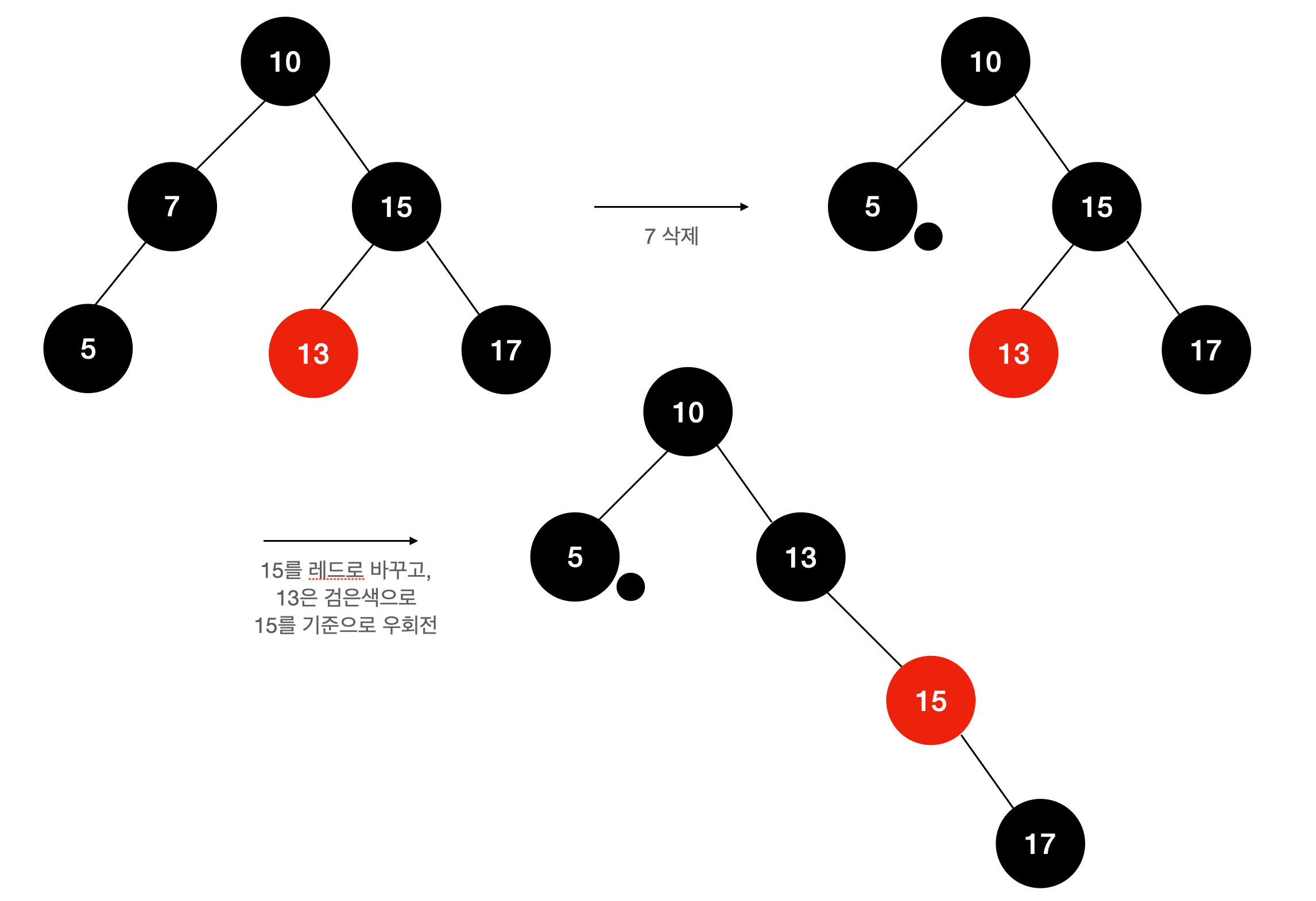
형제 노드의 색을 빨간색, 왼쪽 자식의 색을 검은색으로 바꾼 뒤, 형제 노드를 회전시켜준다.
그 뒤, Case 3으로 넘어간다.
Case 3. 이중 흑색노드의 형제가 검은색, 오른쪽 자식이 빨간색인 경우
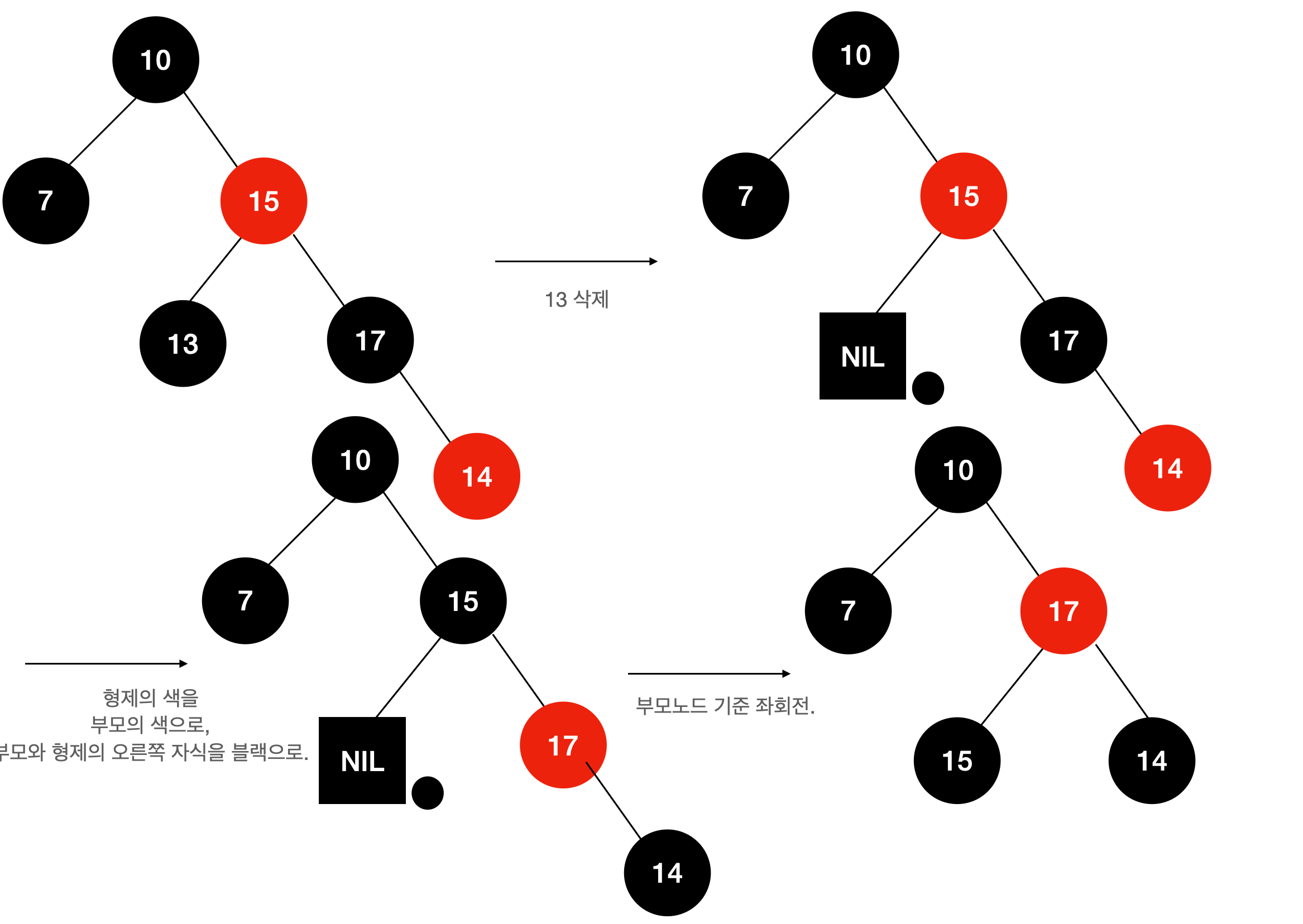
형제의 색을 부모의 색으로 바꿔주고, 부모와 형제의 오른쪽 자식을 검은색으로 칠한다. 그리고 부모노드를 기준으로 좌회전한다.
아래는 이중흑색노드 해결의 슈도코드이다:
delete_fixup(node):
while node != root and node.color == BLACK:
if node == node.parent.left:
sibling = node.parent.right
if sibling.color == RED:
# case 1: sibling이 빨간색인 경우
sibling.color = BLACK
node.parent.color = RED
left_rotate(node.parent)
sibling = node.parent.right
if sibling.left.color == BLACK and sibling.right.color == BLACK:
# case 2: sibling과 sibling의 자식들이 모두 검은색인 경우
sibling.color = RED
node = node.parent
else:
if sibling.right.color == BLACK:
# case 3: sibling의 오른쪽 자식이 검은색인 경우
sibling.left.color = BLACK
sibling.color = RED
right_rotate(sibling)
sibling = node.parent.right
# case 4: sibling의 오른쪽 자식이 빨간색인 경우
sibling.color = node.parent.color
node.parent.color = BLACK
sibling.right.color = BLACK
left_rotate(node.parent)
node = root
else //left와 right를 바꿔서 똑같게'컴퓨터과학 > 자료구조' 카테고리의 다른 글
| [자료구조] 4-9. 힙(Heap)과 우선 순위 큐(Priority Queue) (0) | 2023.04.14 |
|---|---|
| [자료구조] 4-8. 트라이(Trie) (0) | 2023.04.14 |
| [자료구조] 4-6. 레드-블랙트리의 삽입(Insertion in Red-Black Tree) (0) | 2023.04.11 |
| [자료구조] 4-5. 레드-블랙 트리(Red Black Tree) (0) | 2023.02.23 |
| [자료구조] 4-4. AVL 트리 (0) | 2022.12.12 |




