넘치게 채우기
[자료구조] 5. 그래프 이론(Graph Theory) 본문
그래프
그래프는 객체로 나타내는 정점(vertex)와 객체를 연결하는 간선(edge)의 집합으로 구성된다.
G = (V, E) (V = 정점의 집합, E = 간선의 집합)

그래프의 종류
무방향 그래프
두 정점을 연결하는 간선에 방향이 없는 그래프이다. 정점 V1에서 정점 V2로 잇는 것을 표현하는 간선으로
(V1, V2)로 표현한다. (V2, V1)로 표현해도 같은 간선이다.

방향 그래프
두 정점을 연결하는 간선에 방향이 있는 그래프이다. 정점 V1에서 정점 V2로 잇는 것을 표현하는 간선으로
<V1, V2>로 표현한다. <V2, V1>이랑은 다른 간선이다.

완전 그래프
각 정점에서 다른 모든 정점을 연결한 그래프이다. 최대로 많은 간선 수를 가지고 있다.
무방향 완전 그래프에서는 정점이 n개일 때, n(n+1)/2개의 간선을 가진다.
방향 그래프에서는 n(n+1)개의 간선을 가진다.

부분 그래프
원래 그래프에서 정점이나 간선을 일부 제외하여 만든 그래프이다.
G'가 G의 부분그래프라고 할 때, V(G')는 V(G)의 부분집합이고, E(G') 역시 E(G)의 부분집합이다.

가중 그래프
정점을 연결하는 간선에 가중치를 부여한 그래프이다.
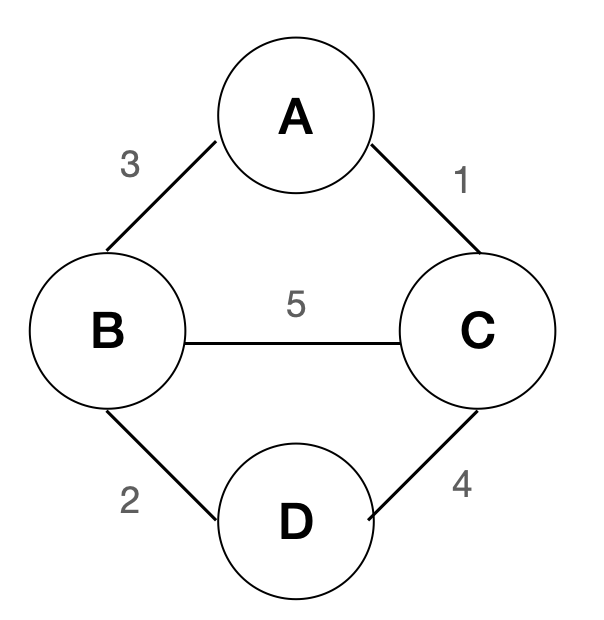
연결 그래프
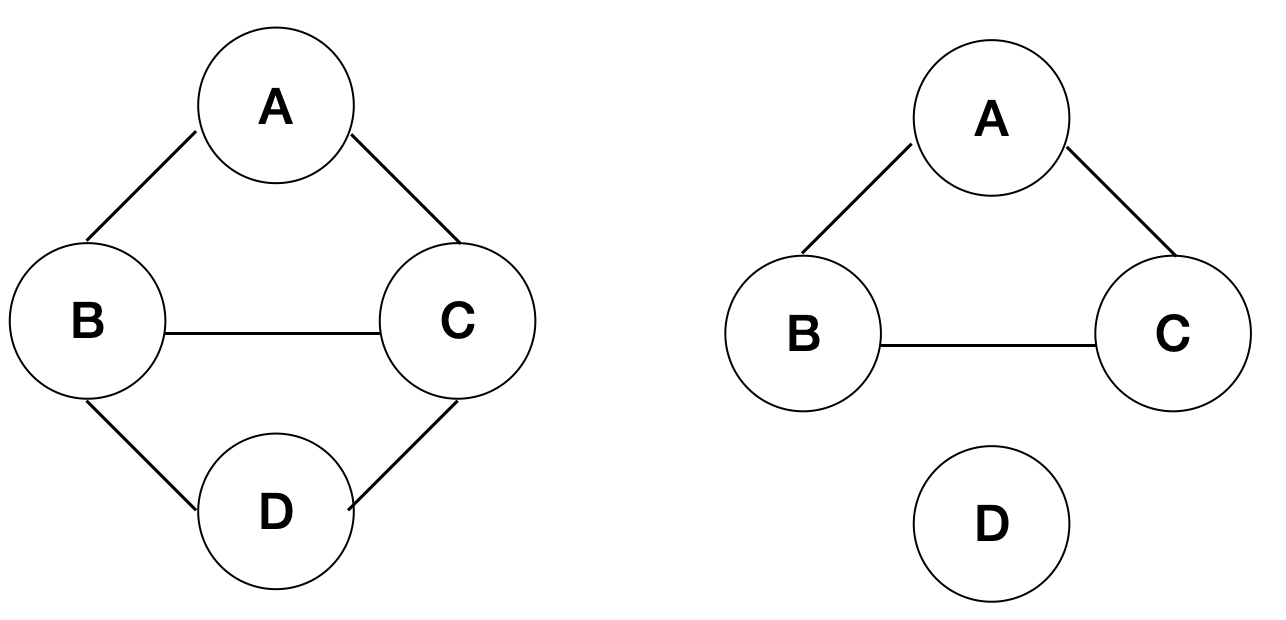
모든 정점들이 간선으로 연결되어 있는 그래프. 트리는 대표적인 연결 그래프의 일종이다.
단절 그래프(비연결 그래프)
떨어져 있는(아무것도 연결되지 않는) 정점이 있는 그래프
그래프 용어
인접: 두 정점 V1, V2가 연결되어 간선 (V1, V2)가 있을때, 두 정점 V1, V2를 인접한다고 한다.
부속: 간선 (V1, V2)는 정점 V1, V2에 부속되어 있다고 한다.
차수: 정점에 부속된 간선의 수를 차수라고 한다.
진입차수: 방향그래프에서 정점을 머리로 하는 간선수이다.
진출차수: 방향그래프에서 정점을 꼬리로 하는 간선수이다.
경로: 정점 V1부터 V2까지의 간선으로 연결한 정점을 순서대로 나타낸 리스트
아래 그림은 A부터 D까지 (A-B-D), (A-B-C-D), (A-C-D), (A-C-B-D)의 경로가 있다.
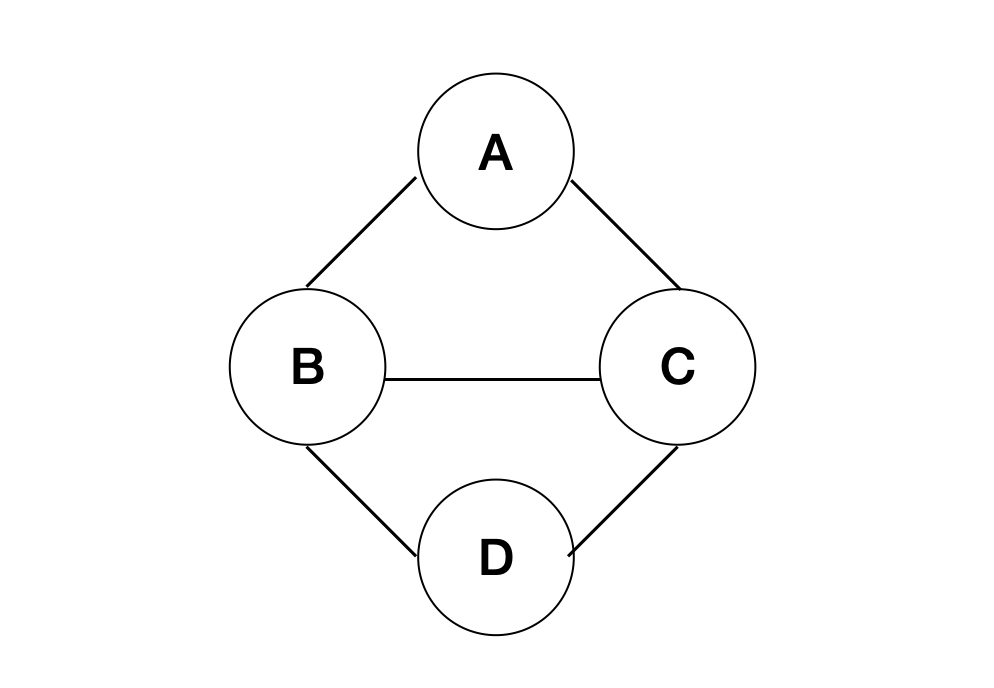
경로 길이: 경로를 구성하는 간선의 수
단순 경로: 모두 다른 정점으로 구성된 경로
사이클: 시작과 끝이 같은 정점인 경로
연결: 두 정점사이에 경로가 있는 관계
DAG: 방향 그래프에서 사이클이 없는 그래프 (Directed Acyclic Graph)
그래프의 구현
인접 행렬
정점을 n개 가진 그래프는 n*n의 정방행렬을 쓰는데, 인접된 관계이면 1, 인접되지 않으면 0으로 나타낸다.
무방향 그래프에서는 간선의 방향이 없어 대칭이 생기고, 방향 그래프에서는 간선의 방향이 있어 대칭하지 않는다.
메모리를 n^2만큼 잡아먹으므로, 간선의 수가 적으면 비효율적이다.
방향 그래프에서 행은 진출차수이고, 열은 진입차수를 의미한다.

인접 리스트
인접 리스트는 각 정점의 인접한 정점들을 연결리스트로 만든다.
리스트 내의 노드는 오름차순으로 연결한다.
정점의 차수만큼 노드가 생긴다.
정점이 n개이고 간선이 e개인 무방향그래프의 인접리스트는 n개의 헤드 포인터와 2e개의 노드가 필요하다.
방향 그래프에서도 n개의 헤드 포인터가 필요하고, 각 노드의 진출차수의 개수만큼 노드가 연결된다.

'컴퓨터과학 > 자료구조' 카테고리의 다른 글
| [자료구조] 두 개의 스택으로 하나의 큐를 구현해보자(향상된 성능으로) (0) | 2024.01.29 |
|---|---|
| [자료구조] 4-9. 힙(Heap)과 우선 순위 큐(Priority Queue) (0) | 2023.04.14 |
| [자료구조] 4-8. 트라이(Trie) (0) | 2023.04.14 |
| [자료구조] 4-7. 레드-블랙 트리의 삭제(Deletion in Red-Black Tree) (0) | 2023.04.12 |
| [자료구조] 4-6. 레드-블랙트리의 삽입(Insertion in Red-Black Tree) (0) | 2023.04.11 |



