넘치게 채우기
세그먼트 트리와 지연전파 (Segment Tree, with lazy propagation) 본문
세그먼트 트리
References:
https://youtu.be/-dUiRtJ8ot0?si=SRjeBHChrzUaN-id
세그먼트 트리란, 1차원 배열에서의 구간 연산에 대해 빠르게 구하는 자료구조이다.
구간 [l, r]에 대해서 기존의 naive하게 업데이트 및 연산하는 것은 O(N)의 시간이 걸리지만,
세그먼트 트리를 이용하면 O(log N)의 시간이 걸린다.
세그먼트 트리는 트리이지만, 배열 기반의 이진트리로 간단하게 표현될 수 있다.
이진트리의 특성상, 0-based의 기준, 인덱스 i 노드의 왼쪽 자식은 i*2+1, 오른쪽 자식은 i*2+2에 위치한다.
1-based의 기준, i노드의 왼쪽 자식은 i*2, 오른쪽 자식은 i*2+1이다.
세그먼트 트리에서,
루트 노드는 모든 구간에 대한 연산 결과를 저장한다.
왼쪽 자식노드는 루트 노드의 왼쪽 절반구간, 오른쪽 자식노드는 부모 노드의 오른쪽 절반구간에 대한 연산 결과를 저장한다.
리프 노드는 원본 배열의 값 하나를 저장한다.
우리는 배열의 크기가 n인경우, 완전 이진 트리를 가정하면 2N-1개가 되는데, 완전 이진트리가 아닐 수 있다.
특정 서브트리가 더 뻗은 형태일 수도 있다. 구현의 편리함을 위해서 4n으로 크기를 잡는다.
이는 안정적인 범위를 보장한다.
대신, 안 쓰는 공간들이 많아지기는 한다.

파란글씨는 인덱스, 노드 아래의 범위는 원본 배열 arr에 대한 범위를 나타낸다.
세그먼트 트리의 인덱스 4번은 구간[0, 2]에 대한
이제, 노드 안의 실제 값을 채워보자.
예를 들어서, 구간에 대한 합을 구한다고 가정해보자.
arr = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}를 가정할 것이다.
여기서는 0-based를 쓸 것이다.
다음과 같이 배열 arr과 seg를 가진다고 가정하자:
int arr[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, seg[40];
세그먼트 트리 초기화하기: build()
배열의 정보를 기반으로, 세그먼트 트리의 노드들을 채워보자.
여기서는 구간에 대한 합을 구하기로 했으므로, 각 서브트리의 루트는 양쪽 자식이 완성되어있어야 채워질 수 있다.
재귀를 이용해서 왼쪽 서브트리와 오른쪽 서브트리를 먼저 완성해야 한다.
루트에서 호출하면, 다음과 같이 자식들을 먼저 완성하기 위해 호출된다.
그렇게, 리프까지 닿게 된다. 여기서는 9번, 16번 노드와 17번 노드에 주목하자.
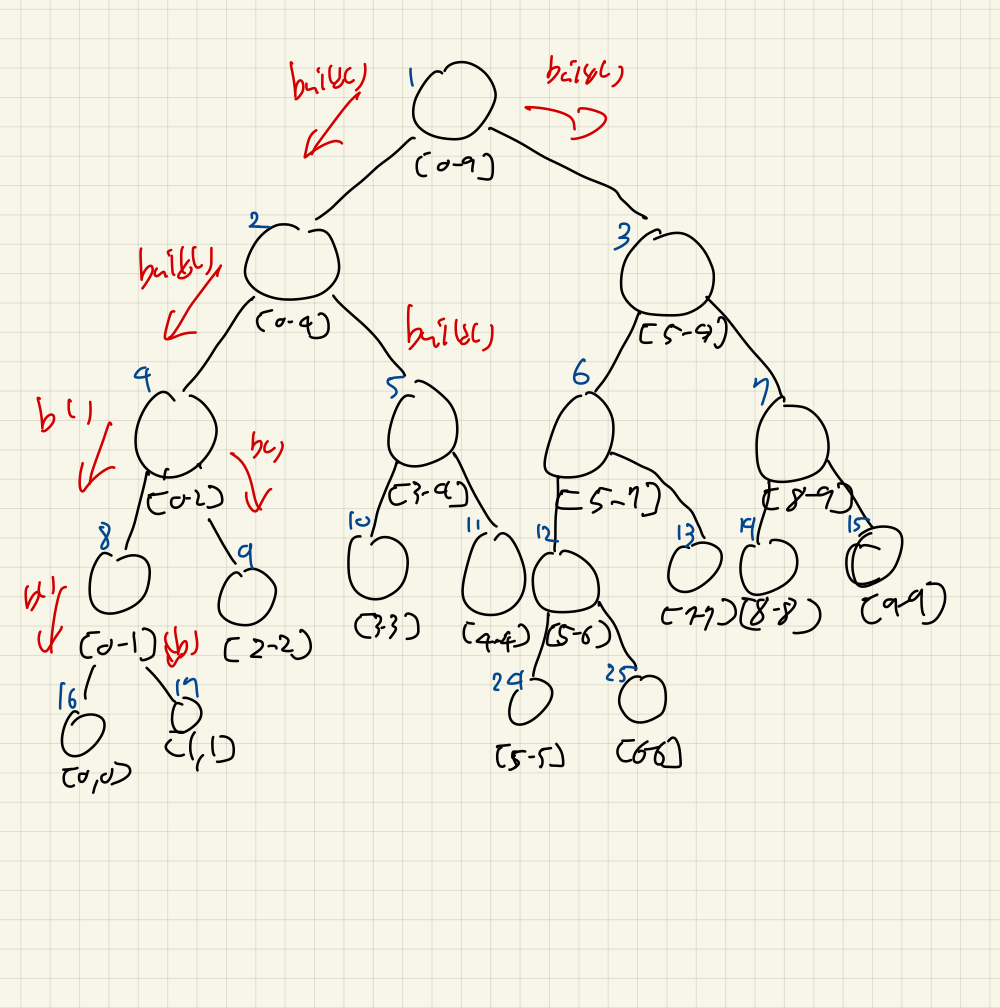
16번 노드와 17번 노드는 리프이다. [l, r]구간에서, l == r이다.
값을 업데이트하고, 탈출한다.
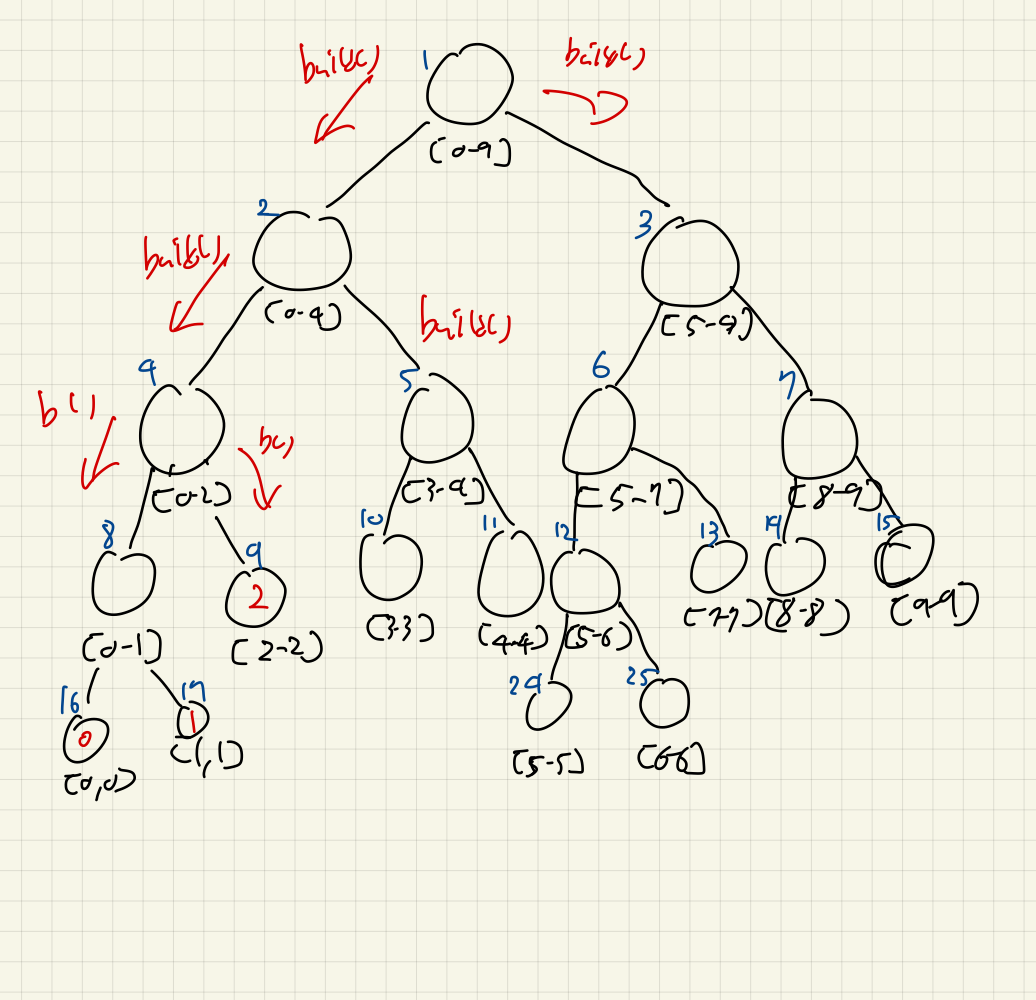
8번 노드는 이제 자식들이 완성되었으므로, 두 자식노드의 합을 구하면, 자신이 맡은 구간에 대한 합이 완성된다.
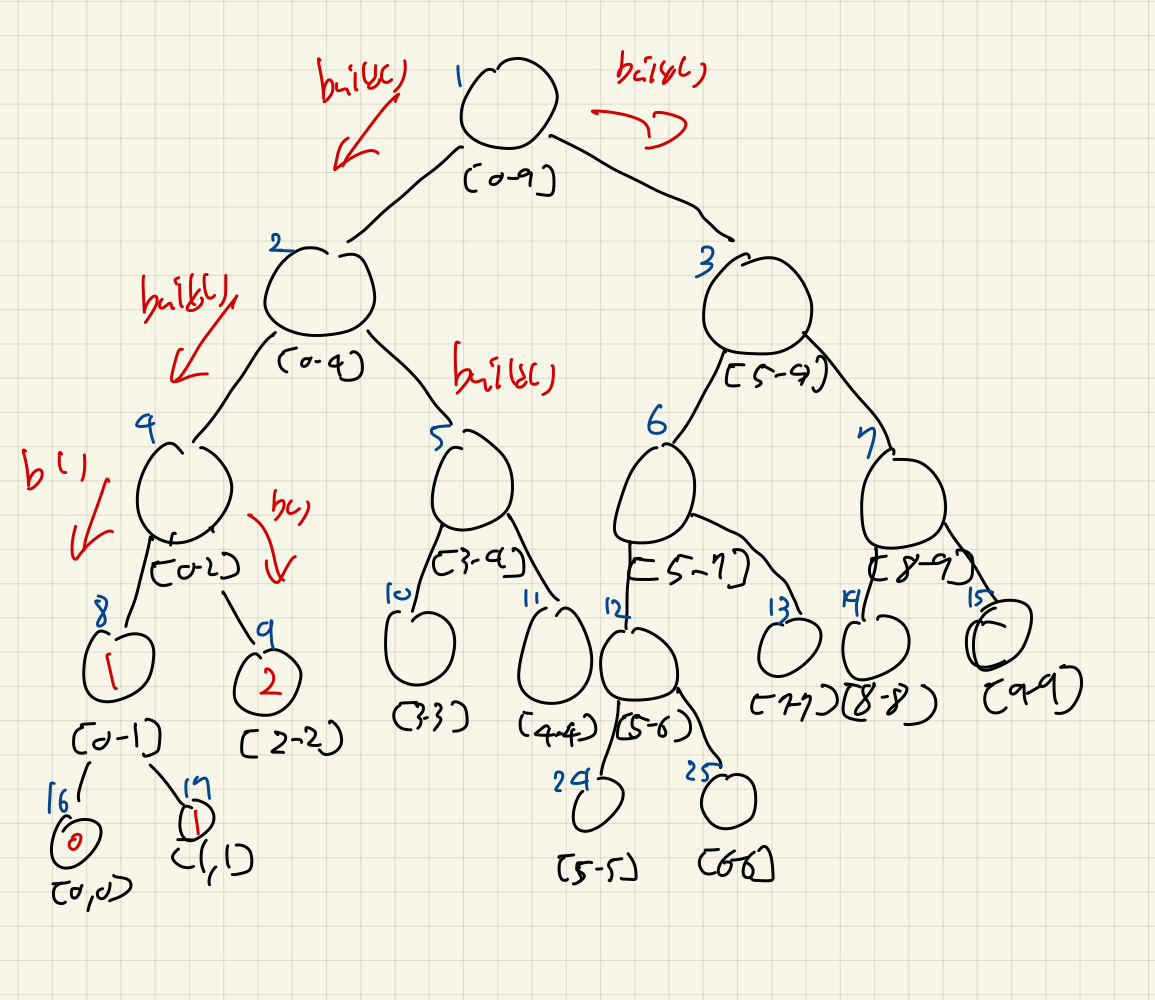
이제, 4번 노드도 양쪽 자식이 완성되었다.
각각의 서브트리들의 반대방향도 똑같이 이와 같은 과정을 거치면, 다음과 같이 완성된다:
([6-6]구간에 0이 아니라 6입니다 양해 바랍니다)
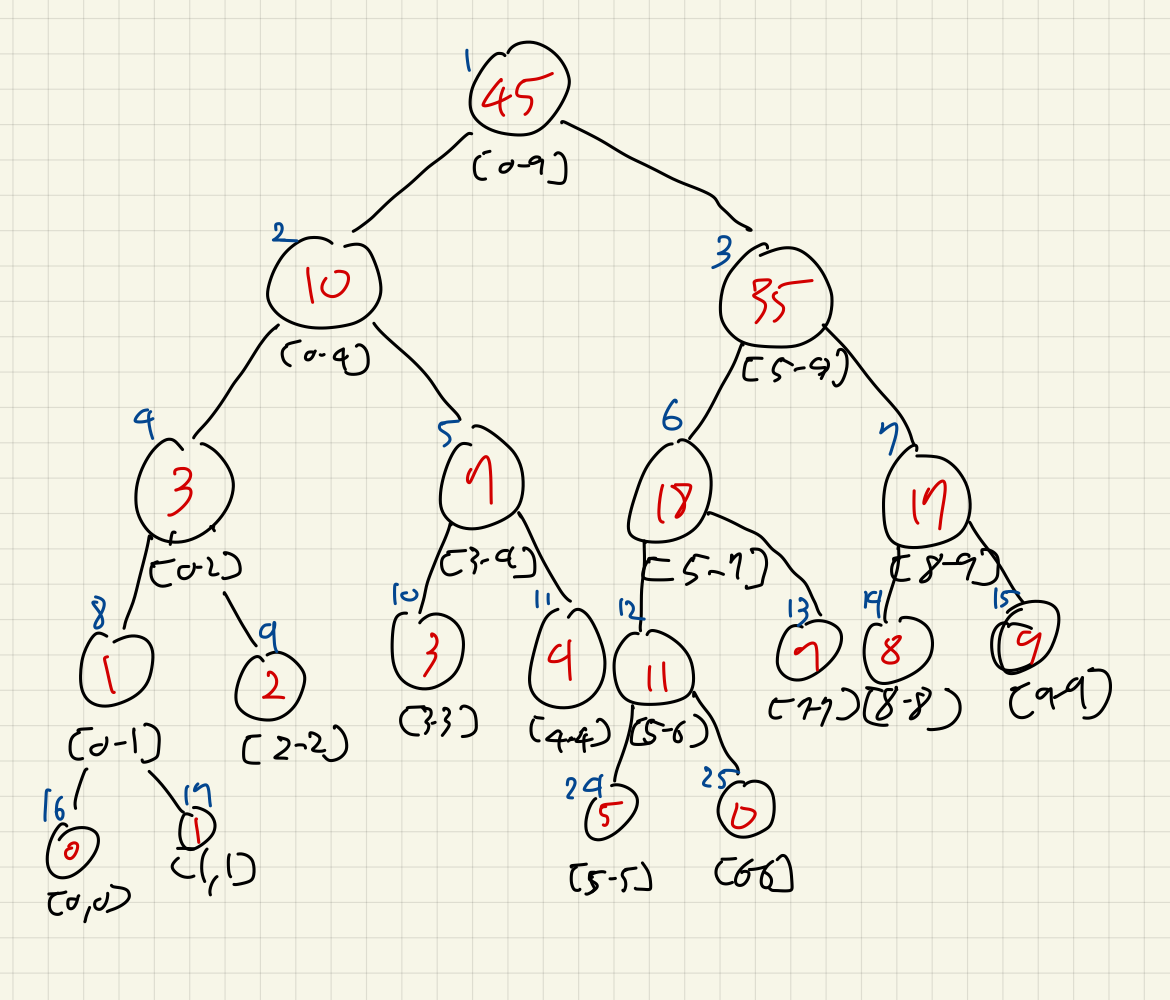
코드 구현:
소스 코드 예시를 보면, 다음과 같다
void build(int index, int l, int r) {
// leaf
if (l == r) {
seg[index] = arr[l];
return;
}
// internal
int mid = (l + r) >> 1;
build(index * 2 + 1, l, mid);
build(index * 2 + 2, mid + 1, r);
seg[index] = seg[index * 2 + 1] + seg[index * 2 + 2];
}
// build(0, 0, n-1);
// 전체 구간에 대해 arr로부터 seg 초기화
세그먼트 트리의 값 업데이트하기: update()
arr의 인덱스 target에 값을 val로 바꿨다고 가정하자.
배열을 바꾸고 build를 호출해도 되겠지만, 불필요한 빌드가 생기게 된다.
인덱스 5의 값이 15로 변경되었다고 가정하자.
우리는 이진트리의 특성으로 인덱스 5의 값이 원래 저장되어있던 리프 노드에 도착할 수 있다.
분할 정복으로, mid보다 작거나 같으면 왼쪽만 호출, mid보다 크면 오른쪽만 호출하면 최소한의 호출로 도달할 수 있다.
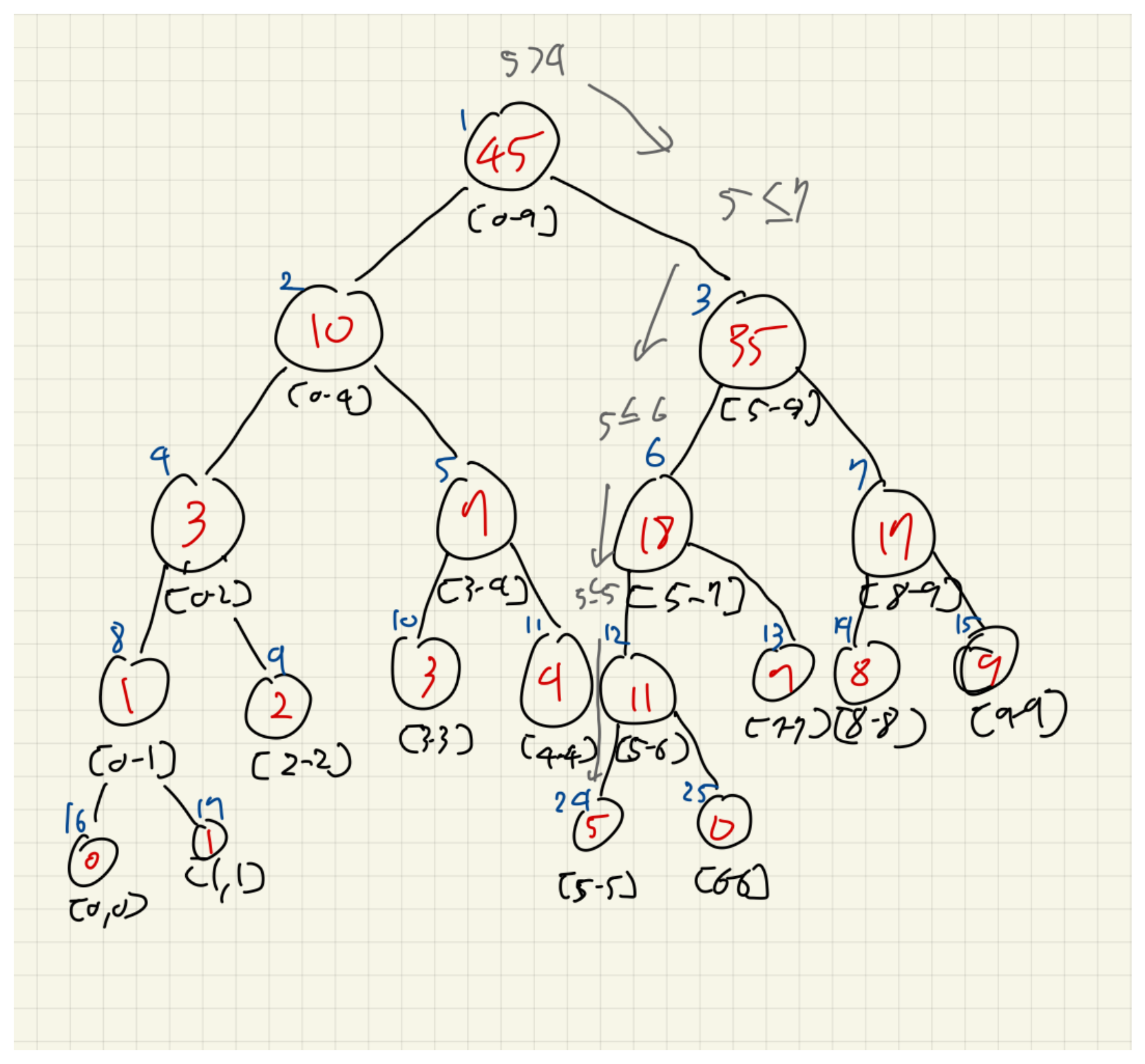
이제, 값을 업데이트하고 다시 재귀호출을 백트래킹하면서 부모노드들의 값을 업데이트해준다.
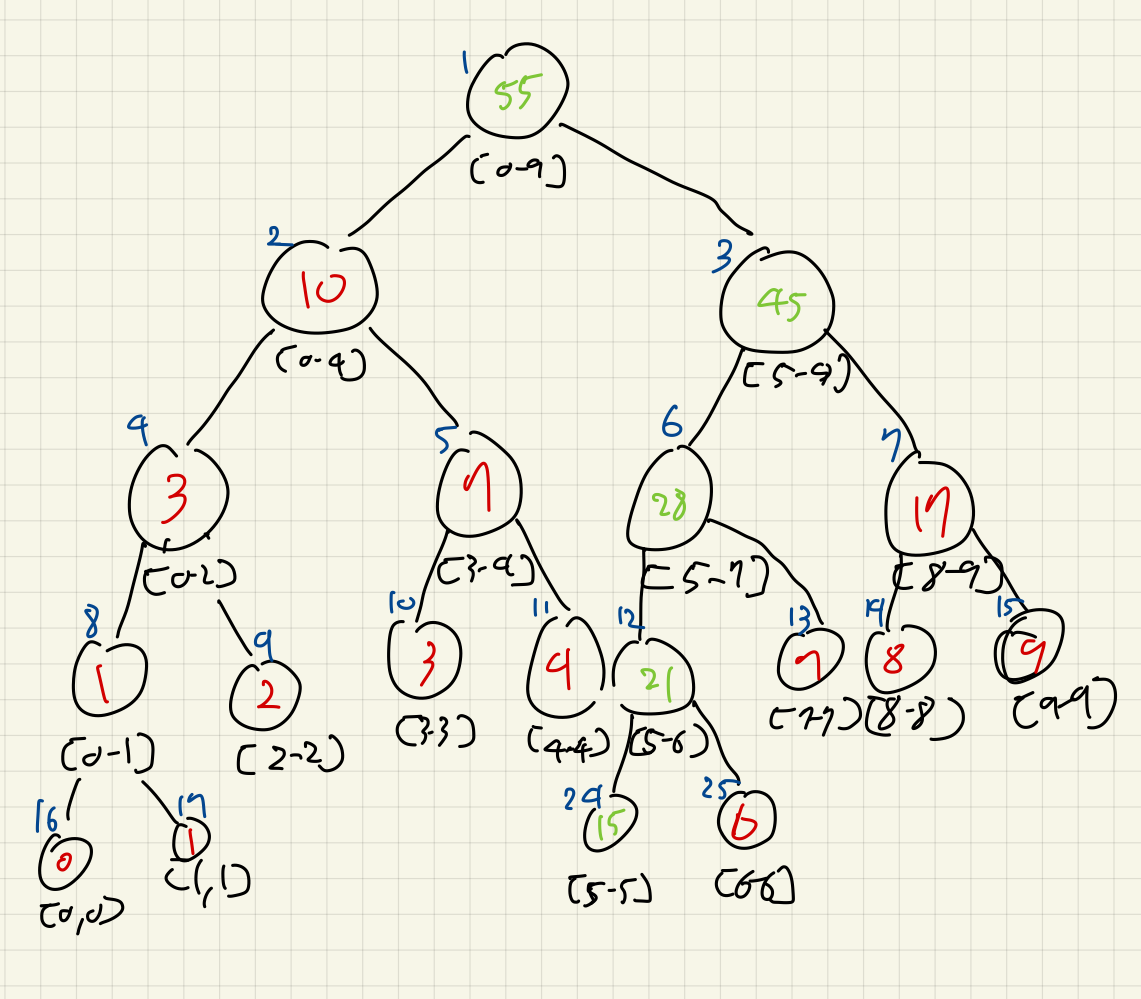
소스 코드 예시를 보면, 다음과 같다:
void update(int index, int target, int val, int l, int r) {
if (l == r) {
seg[index] = val;
return;
}
int mid = (l + r) >> 1;
if (target <= mid) {
update(index * 2 + 1, target, val, l, mid);
} else {
update(index * 2 + 2, target, val, mid + 1, r);
}
seg[index] = seg[index * 2 + 1] + seg[index * 2 + 2];
}
세그먼트 트리에 구간 연산 질의하기: query()
이제, 세그먼트 트리에서 구간합을 빠르게 구해보자.
[2, 8]구간에 대한 구간합을 질의해볼 것이다.
우선, 루트부터 보자.
루트는 [0, 9]구간의 합을 가지고 있다.
[0, 9]구간은 [2, 8]구간에 완전히 포함하지 않는다.
이런 경우, 양쪽의 서브트리에 나눠서 질의해야 한다.
[0, 4]구간과 [5, 9] 구간에 질의해보자.
[0, 4]구간역시 완전히 포함되지 않아서, 양쪽으로 쿼리를 추가로 나눠봐야 한다.
[0, 2]와 [3, 4]로 나눠서 질의한다.
[0, 2]구간역시 완전히 포함되지 않아서, 양쪽으로 쿼리를 나눈다.
[0, 1]구간과 [2, 2]구간으로 나눈다.
[0, 1]구간은 쿼리와 완전히 무관한, 유효하지 않은 구간이다.
우리는 합을 구하는게 목적이므로, 합과는 전혀 무관한 0을 반환하자.
어느 연산을 하느냐에 따라서, 어떻게 반환해야 할지가 달라진다.
[2, 2]구간은 [2, 8]구간에 완전히 포함된다. seg[9(구간의 노드번호)]를 리턴해서 자신이 책임질 수 있는 구간들의 합에 대해 반환한다.
[3, 4]구간은 완전히 포함된다. 똑같이 seg[5]를 반환해준다.
이제, [0, 4]구간에 질의해서 나온 하위 결과들이 도착했다. 두 질의결과인 [2, 4]의 구간합은 9이다.
[5, 9]에 질의해보자.
똑같은 과정을 거쳐서, [6, 8]에 대한 구간합인 36을 얻었다.
루트 [0, 9]에 대해서, 왼쪽 응답인 [2, 4]는 9를, [5, 8]은 36을 답했다.
이를 취합해서, [2, 8]의 합은 45임을 알 수 있다.
아래 그림에 세부적인 과정이 있다.
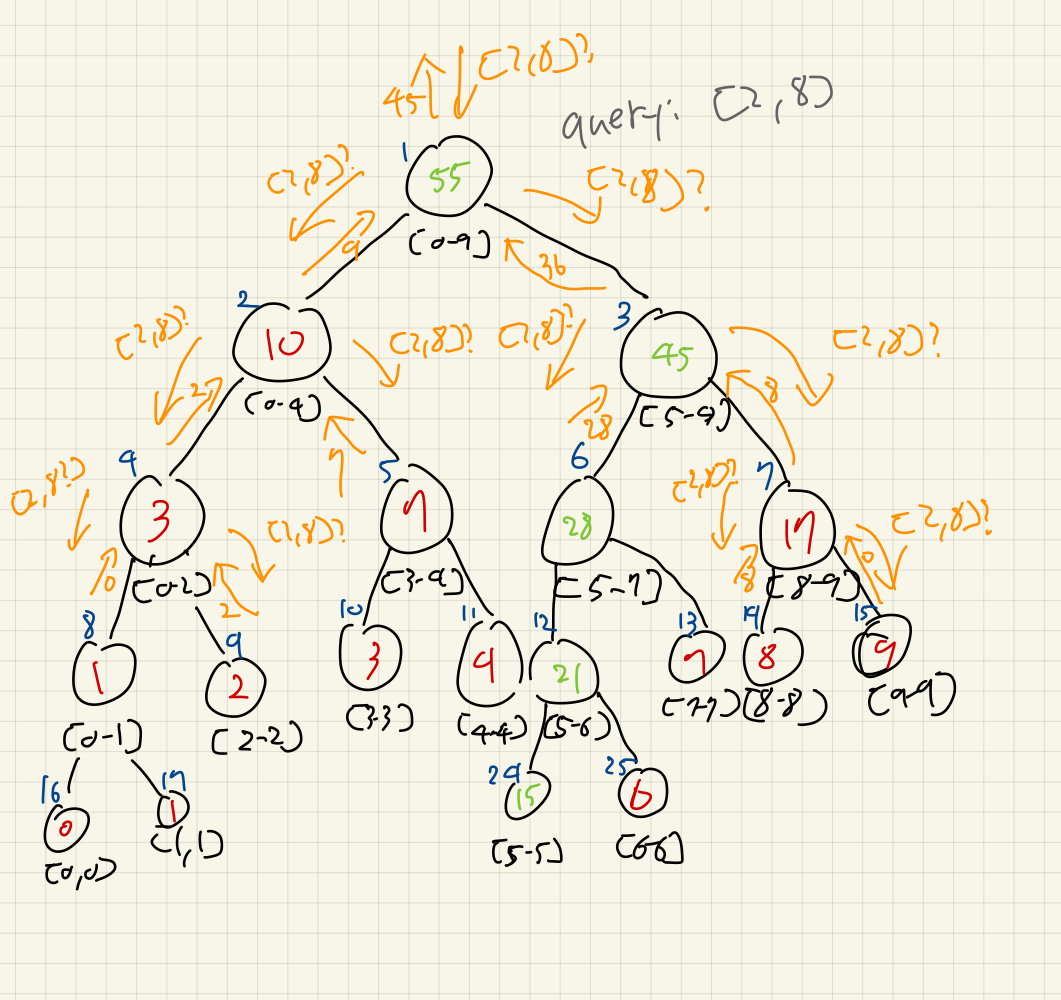
소스 코드 예시는 다음과 같다:
int query(int index, int l, int r, int ql, int qr) {
if (ql > r || qr < l) {
return 0;
}
if (ql <= l && r <= qr) {
return seg[index];
}
int mid = (l + r) >> 1;
int lres = query(index * 2 + 1, l, mid, ql, qr);
int rres = query(index * 2 + 2, mid + 1, r, ql, qr);
return lres + rres;
}
전체 코드 예시
전체 코드 예시는 다음과 같다:
#include <bits/stdc++.h>
using namespace std;
int arr[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, seg[40];
void build(int index, int l, int r) {
// leaf
if (l == r) {
seg[index] = arr[l];
return;
}
// internal
int mid = (l + r) >> 1;
build(index * 2 + 1, l, mid);
build(index * 2 + 2, mid + 1, r);
seg[index] = seg[index * 2 + 1] + seg[index * 2 + 2];
}
void update(int index, int target, int val, int l, int r) {
if (l == r) {
seg[index] = val;
return;
}
int mid = (l + r) >> 1;
if (target <= mid) {
update(index * 2 + 1, target, val, l, mid);
} else {
update(index * 2 + 2, target, val, mid + 1, r);
}
seg[index] = seg[index * 2 + 1] + seg[index * 2 + 2];
}
int query(int index, int l, int r, int ql, int qr) {
if (ql > r || qr < l) {
return 0;
}
if (ql <= l && r <= qr) {
return seg[index];
}
int mid = (l + r) >> 1;
int lres = query(index * 2 + 1, l, mid, ql, qr);
int rres = query(index * 2 + 2, mid + 1, r, ql, qr);
return lres + rres;
}
int main() {
int n = 10;
build(0, 0, n - 1);
cout << "Sum of range (2, 8): " << query(0, 0, n - 1, 2, 8) << endl;
cout << "Updating index 5 to 15..." << endl;
update(0, 5, 15, 0, n - 1);
cout << "Sum of range (2, 8) after update: " << query(0, 0, n - 1, 2, 8)
<< endl;
return 0;
}
출력:
❯ g++ -std=c++17 -o segtree.out segtree.cpp && ./segtree.out
Sum of range (2, 8): 35
Updating index 5 to 15...
Sum of range (2, 8) after update: 45
💤지연전파를 동반한 세그먼트 트리(Segment Tree with Lazy Propagation)
Refernece:
https://www.youtube.com/watch?v=rwXVCELcrqU
이제 우리는 구간 연산에 대해 O(log n)으로 구할 수 있게 되었다.
이전의 업데이트는 단일 요소만 변경하였는데, 구간에 대해서 변경할 수 없을까?
k번 하는 경우, O(k log n)으로, 이는 너무 느리다.
대신, 가상의 lazy라는 트리를 이용해서 빠른 업데이트를 진행할 것이다.
당장 쿼리에 필요한 부분만 업데이트하고, 필요없는 부분은 업데이트를 미루는 방식이다.
lazy는 세그먼트 트리와 똑같은 모양으로, 값에는 나중에 업데이트를 반영할 누적값을 담을 것이다.
lazy 배열을 만들어준다. 세그먼트 트리와 대응되는 구조를 가진다.
int arr[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, seg[40], lazy[40];
lazy propagation을 동반한 수정된 update()
만약에, [ql, qr]구간에 대해서, val만큼 더한다고 가정해보자.
우리는 기존의 세그먼트 트리에서, 쿼리에 대해 어떻게 처리했는지 알 수 있다.
완전히 포함되는 범위에서 값을 리턴했었다.
lazy propagation도 유사하게, 완전히 포함되는 범위에서만 값을 업데이트하고, 서브트리에 대해서는 미룬다.
만약 [5, 8]구간에 대해 모두 +2를 하도록 업데이트를 요청한다고 해보자.
[0, 4]구간의 노드는 일단 자신이 미뤄둔 전파에 대해 업데이트를 반영하지만, 미뤄둔 변경사항도 없고, 아무것도 할 필요가 없어서 리턴한다.
[5, 9]에 대해서도 호출한다.
(지금은 전파 업데이트라는 말을 무시하자. 조금 뒤에 볼 것이다.)
![세그먼트트리 [5,8] lazy propagation update -1](https://blog.kakaocdn.net/dn/cbE1fl/btsMnMIVOUX/D3DPHzdJ9K2m9XSbr9nH5K/img.png)
우선, [5, 9]의 왼쪽자식인 [5, 7]부터 호출한다.
역시 이전의 미뤄둔 전파는 없어 하지 않는다.
그리고, [5, 7]은 [5, 8]에 완전히 소속된다.
여기서, 더 이상 내려가지 않고, lazy배열에 증가값 2를 넣는다.
노드 옆에 작게 쓰여진 초록색 노드가 lazy 가상 트리의 노드라고 보면 된다.
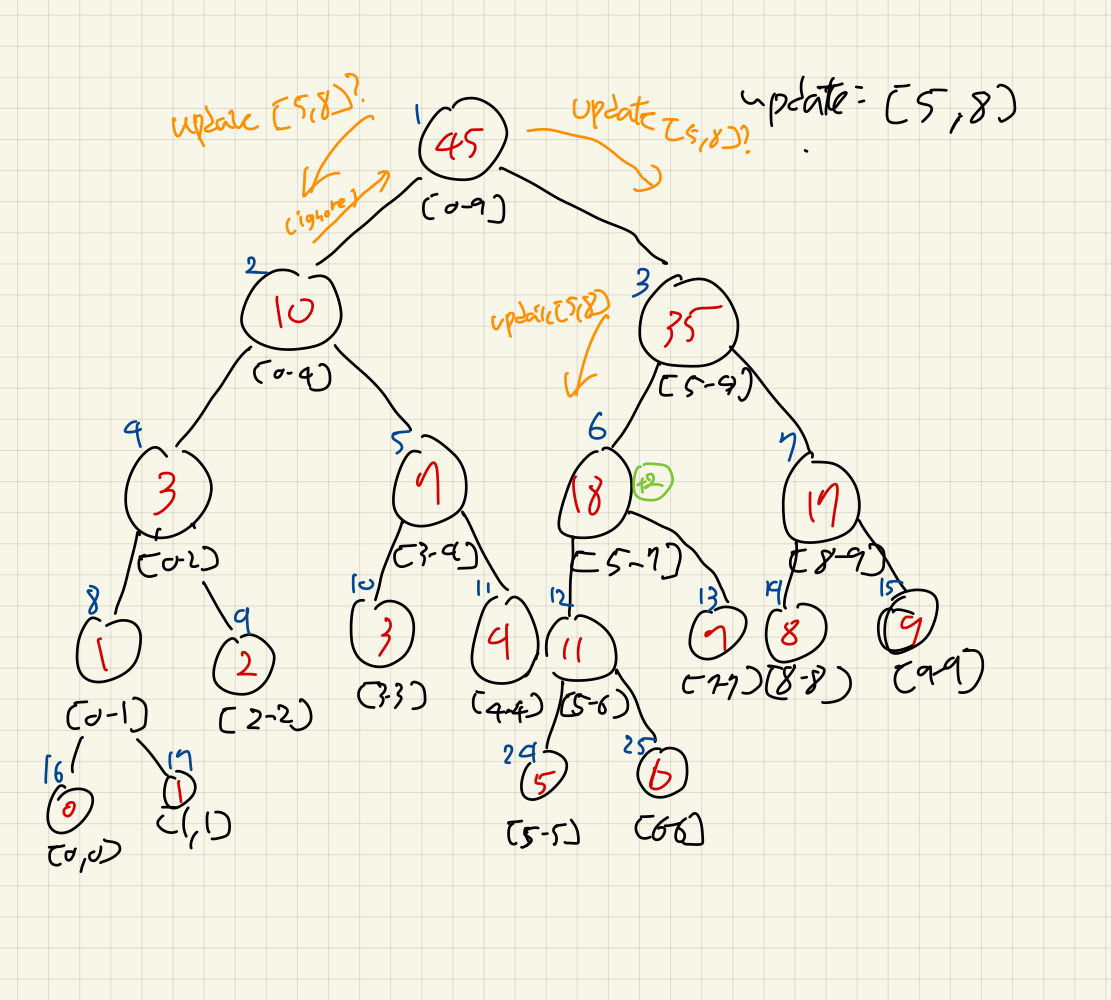
그 뒤, 전파 작업을 진행한다.
현재 lazy에 누적된 만큼 범위에 선반영을 해줄것이다. 하위 노드들의 연산을 하지 않고 말이다.
+2를 [5-7]의 범위에 하므로, 2*(7-5+1) = 6, 즉 6이 증가된 것을 이 노드에서 선반영한다.
하위 노드들에는 아직 적용되지 않았다. 현재는 쓸 일이 없는 노드이므로, 더 미룰 것이다.
그래서, 두 자식 노드들에게 lazy값을 그대로, 즉 2를 물려준다.
[5, 7]에 붙어있던 +2가 아래 두 자식에게 전파되고, 노드 스스로는 값의 증가가 선반영됨을 확인하자.
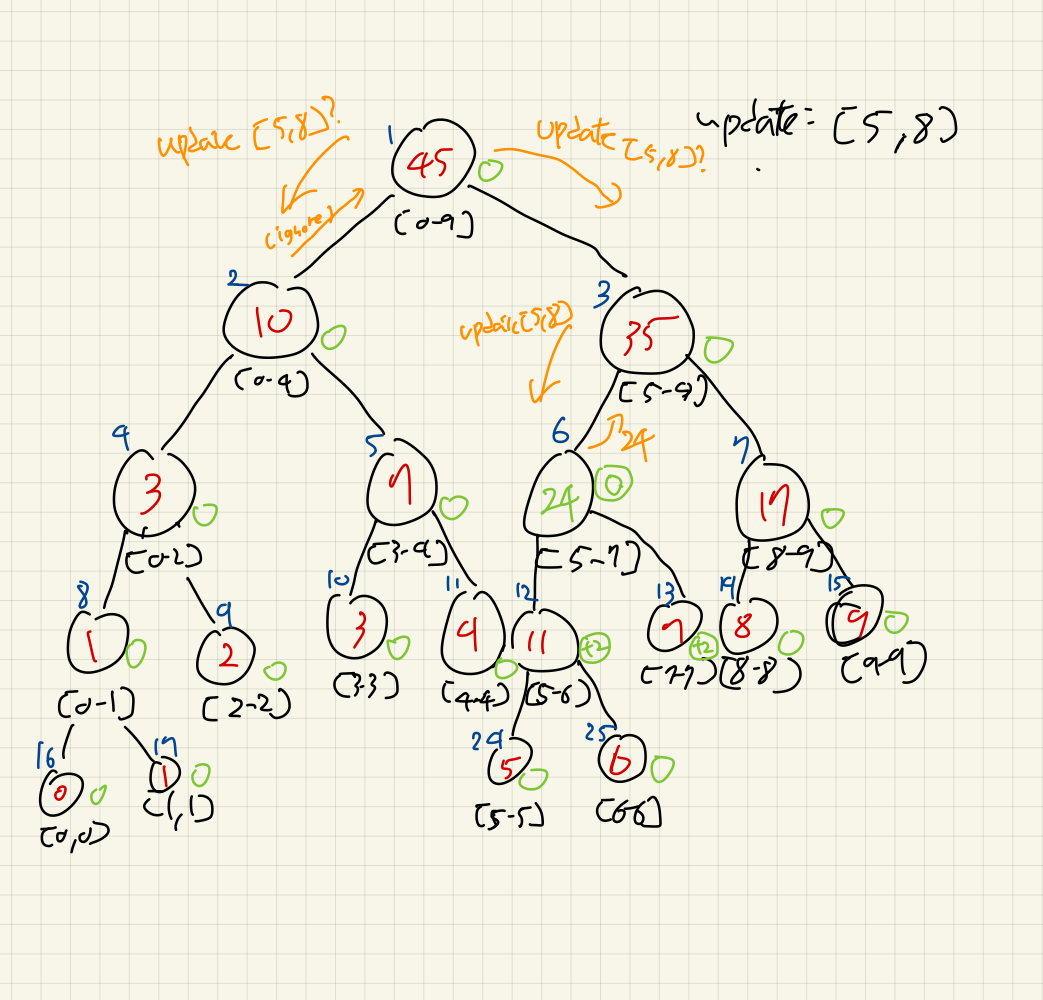
이번에는 [8, 9]로 업데이트를 호출한다. [8, 8]부분 먼저 확인해보자.
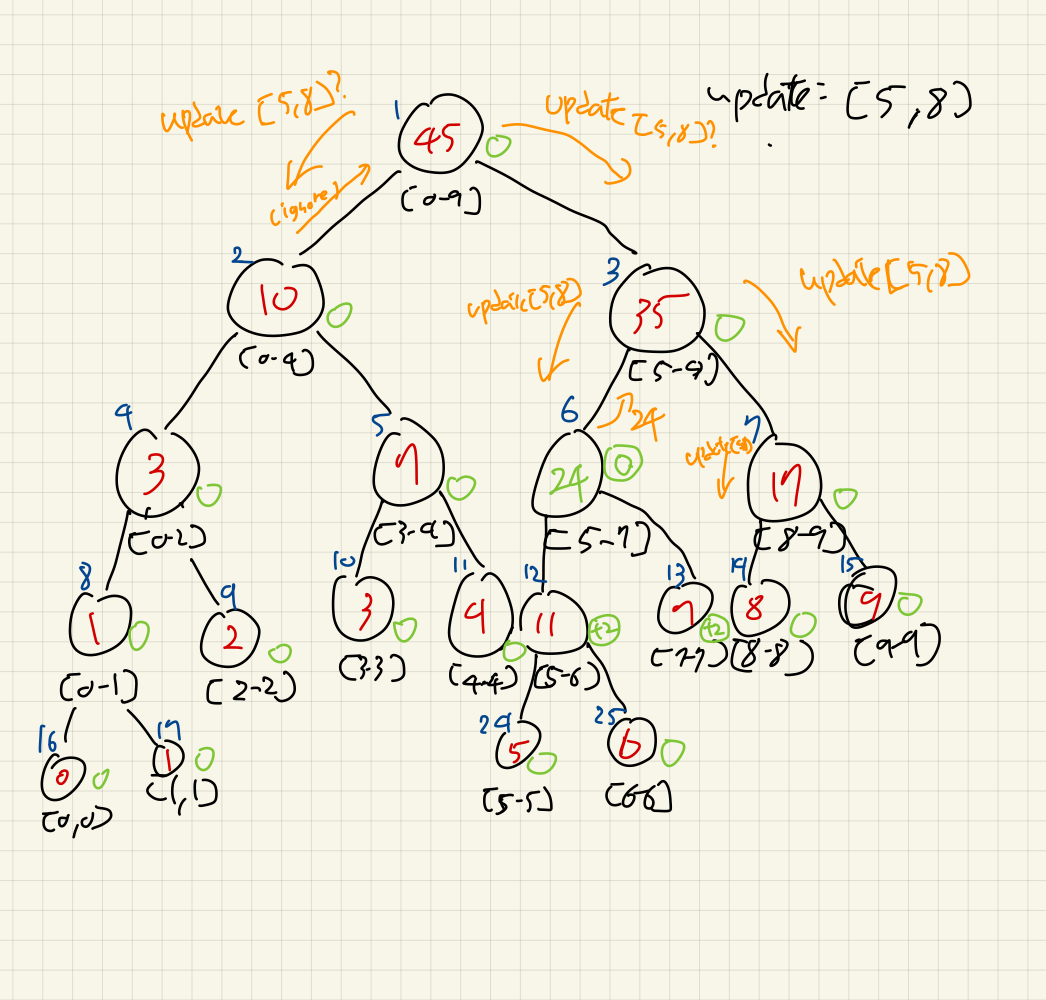
포함되는 범위인 [8, 8]에 도착했다.
lazy에 값을 추가하고, 위에서처럼 똑같이 전파를 시도한다.
단, 이 노드는 리프 노드이므로, 자식 노드에 전파를 하지는 않고, 변경사항만 반영한다.
반대편 [9, 9]는 해당사항이 없는 범위이다.
lazy전파만 진행하고, 돌아온다.
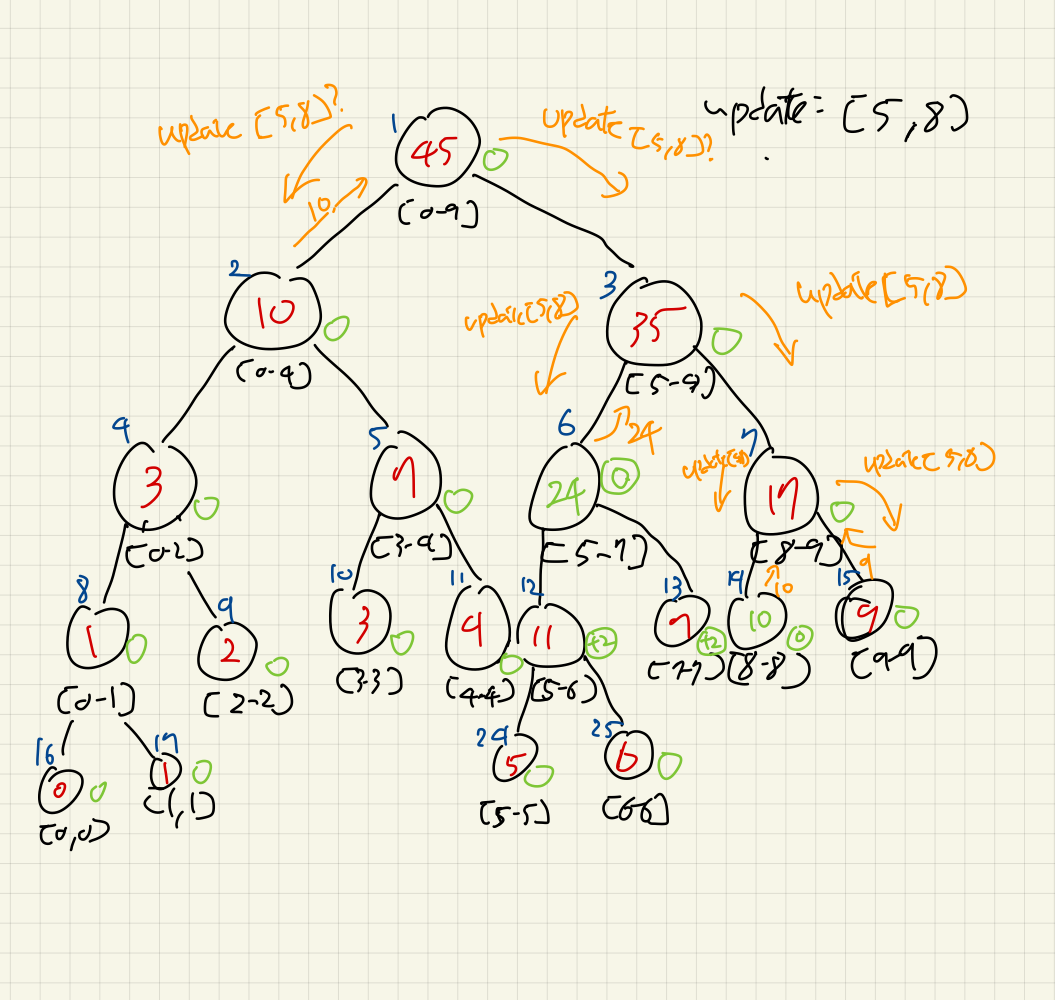
이제 연쇄적으로 자식노드들이 완성되면서, 부모노드들의 업데이트가 한번 더 진행된다.
[8, 9], [5, 9], [0, 9]순서대로 자식들의 값을 참조하여 새로 반영한다.
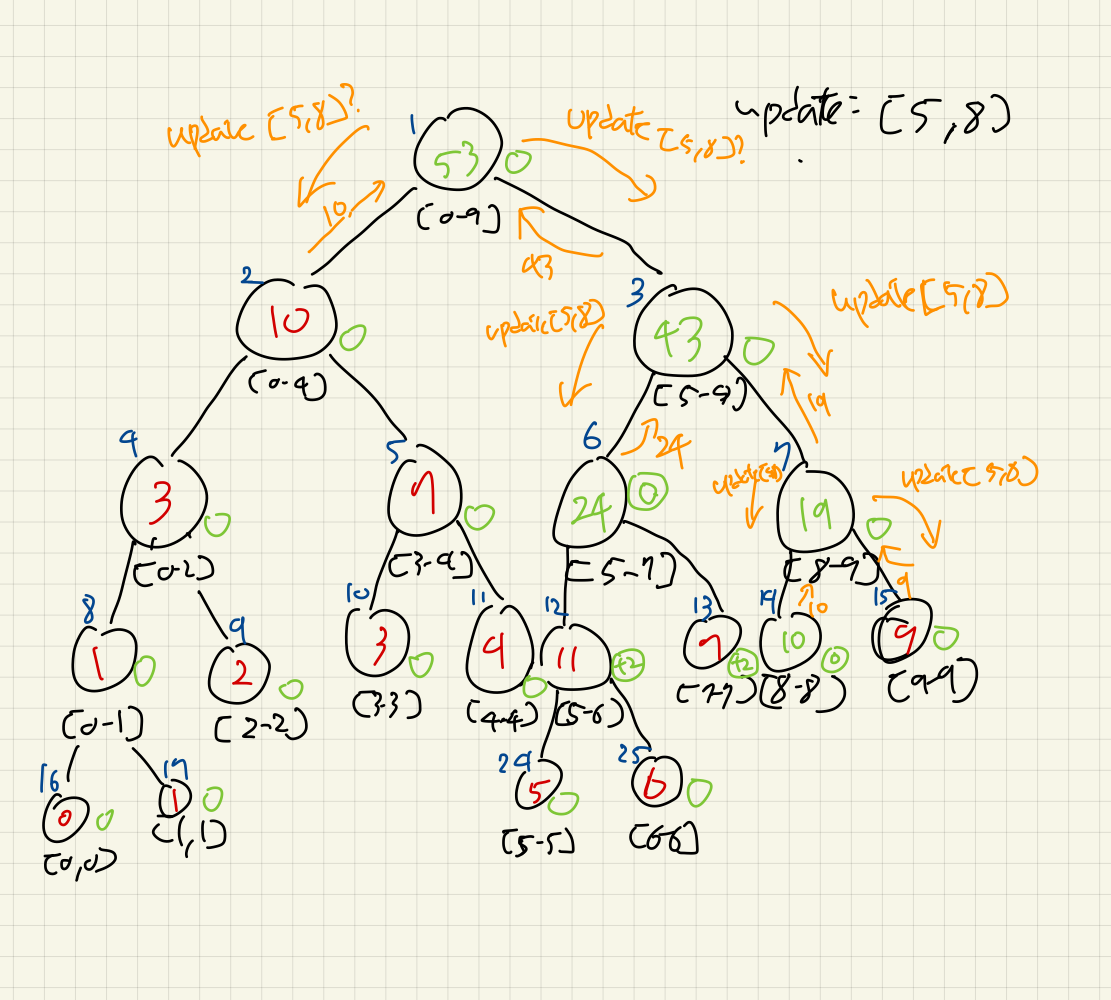
설명에서는 일부 생략되어 전파가 유효한 범위에서만 되거나 내부 노드에서는 안 되는줄로 오해할 수 있지만, 혹시 모를 쌓여있는 lazy누적값들이 있을 수 있으므로, update함수 호출 맨 처음으로 전파를 진행한다.
이는 범위에 상관없이 호출된다.
그렇지 않으면, 잘못된 값이 남아있을 수 있다. 한 번 탐색된 노드에서는 우선 lazy값을 밀어내야 한다고 보면 된다.
코드 예시는 다음과 같다:
void propagate(int index, int l, int r) {
if (lazy[index] != 0) {
seg[index] += lazy[index] * (r - l + 1);
if (l != r) {
lazy[index * 2 + 1] += lazy[index];
lazy[index * 2 + 2] += lazy[index];
}
lazy[index] = 0;
}
}
void update(int index, int l, int r, int ql, int qr, int val) {
propagate(index, l, r);
if (ql > r || qr < l) {
return;
}
if (ql <= l && r <= qr) {
lazy[index] += val;
propagate(index, l, r);
return;
}
int mid = (l + r) >> 1;
update(index * 2 + 1, l, mid, ql, qr, val);
update(index * 2 + 2, mid + 1, r, ql, qr, val);
seg[index] = seg[index * 2 + 1] + seg[index * 2 + 2];
}
lazy propagation을 동반한 수정된 query()
여기서도 원칙은 같다.
범위가 유효하던 유효하지 않던, 현재 노드에서 쌓여있는 Lazy값들을 반영하고, 자식노드들에게 떠넘기는 전파작업을 먼저 하고,
그 이후로는 기존의 query작업과 같다.
이번에는 [3, 6]에 대한 구간합을 구해보자.
우선, [3, 4]구간에 대해서는 빠르게 생략했다.
바로 [5, 6]부분에 주목하도록 전과정을 건너뛴 모습이 아래 그림에 나타나져 있다:
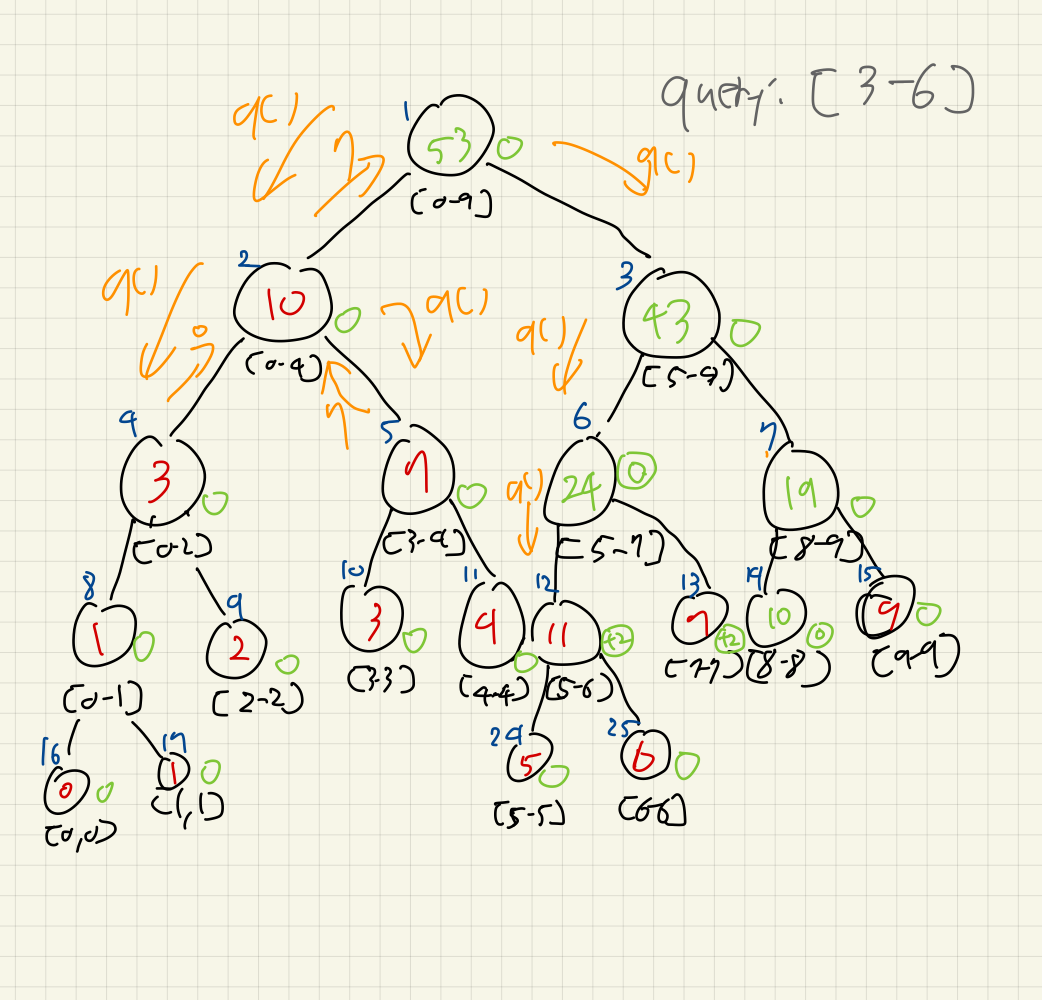
이제, [5, 6]구간은 완전히 포함되는 구간이므로, 여기서의 seg값을 반환하면 되지만, lazy값이 있음을 알 수 있다.
우리는 방문한 노드에 대해서 반드시 lazy값으로 선반영하고 밀어내야 한다는 것을 알았다.
노드 값에 2*(6-5+1) = 4를 더하고, lazy값 2를 자식노드들에게 전파한다.
아래 그림은 전파 이후 상위 노드에 서브쿼리를 리턴하는 끝까지의 과정을 보인다.
쿼리 결과는 7 + 15로, 22가 나온다.
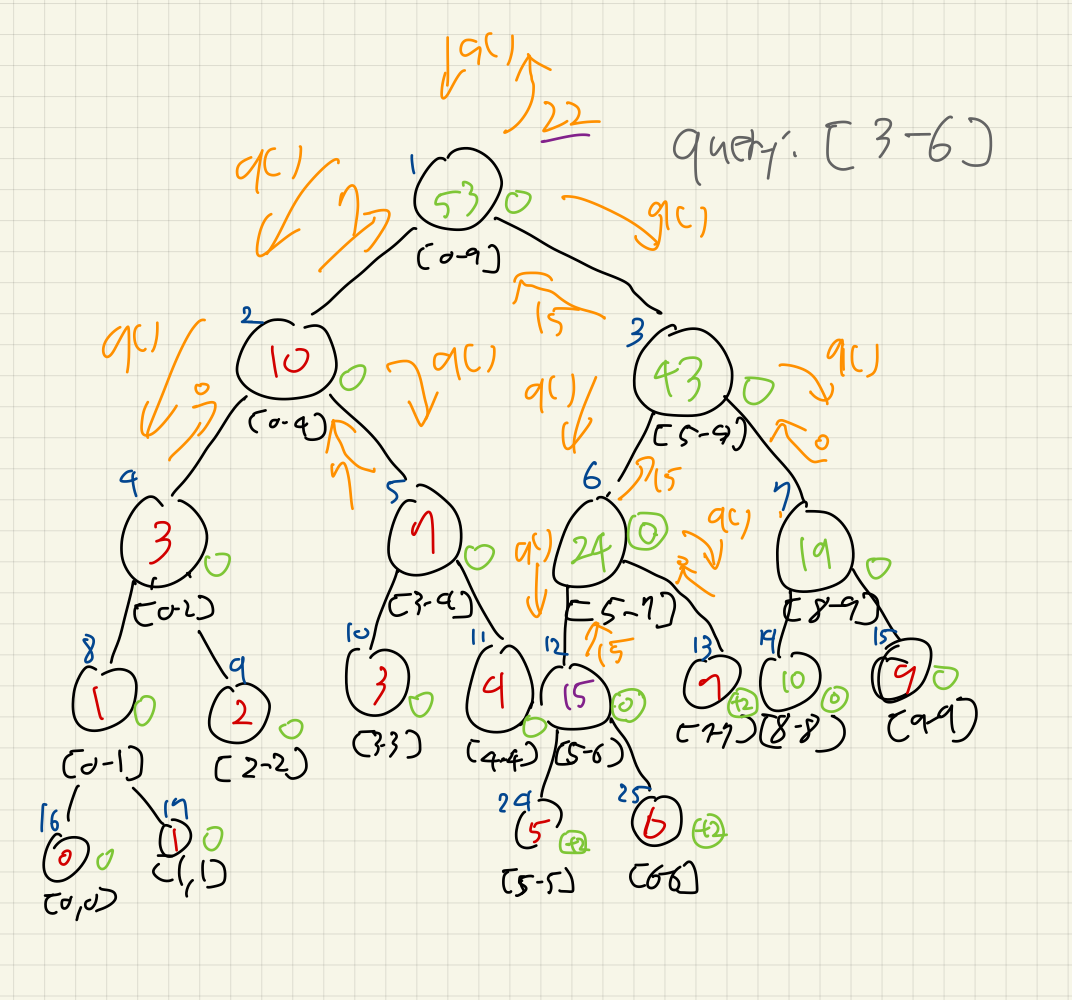
query의 코드는 다음과 같다:
int query(int index, int l, int r, int ql, int qr) {
propagate(index, l, r);
if (ql > r || qr < l) {
return 0;
}
if (ql <= l && r <= qr) {
return seg[index];
}
int mid = (l + r) >> 1;
int lres = query(index * 2 + 1, l, mid, ql, qr);
int rres = query(index * 2 + 2, mid + 1, r, ql, qr);
return lres + rres;
}
lazy propagation을 적용한 전체 코드 예시
#include <bits/stdc++.h>
using namespace std;
int arr[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, seg[40], lazy[40];
void build(int index, int l, int r) {
// leaf
if (l == r) {
seg[index] = arr[l];
return;
}
// internal
int mid = (l + r) >> 1;
build(index * 2 + 1, l, mid);
build(index * 2 + 2, mid + 1, r);
seg[index] = seg[index * 2 + 1] + seg[index * 2 + 2];
}
void propagate(int index, int l, int r) {
if (lazy[index] != 0) {
seg[index] += lazy[index] * (r - l + 1);
if (l != r) {
lazy[index * 2 + 1] += lazy[index];
lazy[index * 2 + 2] += lazy[index];
}
lazy[index] = 0;
}
}
void update(int index, int l, int r, int ql, int qr, int val) {
propagate(index, l, r);
if (ql > r || qr < l) {
return;
}
if (ql <= l && r <= qr) {
lazy[index] += val;
propagate(index, l, r);
return;
}
int mid = (l + r) >> 1;
update(index * 2 + 1, l, mid, ql, qr, val);
update(index * 2 + 2, mid + 1, r, ql, qr, val);
seg[index] = seg[index * 2 + 1] + seg[index * 2 + 2];
}
int query(int index, int l, int r, int ql, int qr) {
propagate(index, l, r);
if (ql > r || qr < l) {
return 0;
}
if (ql <= l && r <= qr) {
return seg[index];
}
int mid = (l + r) >> 1;
int lres = query(index * 2 + 1, l, mid, ql, qr);
int rres = query(index * 2 + 2, mid + 1, r, ql, qr);
return lres + rres;
}
int main() {
int n = 10;
build(0, 0, n - 1);
cout << "Initial sum (0-9): " << query(0, 0, n - 1, 0, 9) << endl;
update(0, 0, n - 1, 2, 5, 3);
cout << "After update (5-8) += 2, sum (0-9): " << query(0, 0, n - 1, 0, 9)
<< endl;
cout << "Query (3-6): " << query(0, 0, n - 1, 3, 6) << endl;
return 0;
}
결과
❯ g++ -std=c++17 -o segtree.out segtree.cpp && ./segtree.out
Initial sum (0-9): 45
After update (5-8) += 2, sum (0-9): 53
Query (3-6): 22
lazy propagation이 항상 옳을까?
항상 옳지는 않다. 업데이트가 누적인 연산 및, 구간 업데이트가 많은 경우에서만 효과적임을 알 수 있다.
그리고, 단일 값에 대한 질의에서는 별 의미가 없음을 알 수 있다.
업데이트값이 누적이 아닌 gcd나 min, max 등의 연산, 또는 제곱, 로그와 같은 비선형적인 연산에는 적합하지 못하다.
적절한 상황에만 쓰여야 한다.
'컴퓨터과학 > 알고리즘' 카테고리의 다른 글
| MITM(Meet-in-the-Middle): n <= 40에 대한 Subset Sum 문제를 위한 방법 (0) | 2024.12.06 |
|---|---|
| LIS(Longest Increasing Subsequence) - O(nlogn)으로 진짜 LIS를 구하기 (0) | 2024.10.21 |
| 오일러 경로와 오일러 회로(Eulerian Trail, Eulerian Circuit) (0) | 2024.10.16 |
| 문자열 패턴 검색: 3 - KMP 알고리즘 (0) | 2024.09.20 |
| 문자열 패턴 검색: 2 - 라빈-카프 알고리즘 (Rabin-Karp Algorithm) (0) | 2024.09.20 |

