넘치게 채우기

https://www.geeksforgeeks.org/introduction-to-disjoint-set-data-structure-or-union-find-algorithm/ Introduction to Disjoint Set (Union-Find Algorithm) - GeeksforGeeks A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions. www.geeksforgeeks.o..

벨만-포드 알고리즘이란? 한 노드에서 다른 노드까지의 최단 거리를 구하는 알고리즘이다. 다익스트라 알고리즘과의 비교 다익스트라 알고리즘은 양수일 때에만 사용이 가능하지만, 벨만포드 알고리즘은 음수에서도 사용이 가능하다. 시간 복잡도는 다익스트라 알고리즘이 더 효율적이다. 벨만포드 알고리즘 1. 시작 노드를 설정한다. 2. 시작 노드를 제외한 모든 노드의 거리를 INF로 구성한다. 3. 현재 노드의 모든 인접 노드를 탐색하며 기존의 연결 관계보다 현재 노드를 거치고 가는 것이 더 짧을 경우 갱신한다. 4. 모든 노드에 대해 반복한다. 5. 모든 노드에 대해 반복하고 나서도 갱신된다면, 그건 음수 사이클이 존재한다는 의미이다. 벨만포드 알고리즘 예시 1.노드 A에서부터 시작한다. 2 < INF, 4 < IN..

순서가 정해져 있는 일련의 알고리즘을 수행해야 할 때 사용되는 알고리즘이다. '사이클이 없는 방향 그래프의 모든 노드를 순서대로 나열하는 것' 이다. 대표적으로 선수학습 과목 등의 예시가 있다. 진입차수와 진출차수 진입차수(indegree): 특정 노드로 들어오는 간선의 개수(노드로 오기 전의 조건) 진출차수(outdegree): 특정 노드에서 나가는 간선의 개수 위상 정렬 알고리즘 1. 진입차수가 0인 노드를 큐에 넣는다. 2. 큐가 빌 때까지 다음의 과정 반복: 큐에서 원소를 꺼내서 그 노드가 향하는 노드의 진입차수를 1 낮추기(그 간선 방문처리) 진입차수가 0이 된 노드를 큐에 넣기 위상 정렬 알고리즘의 예시 1. 진입차수가 0인 노드부터 큐에 넣고 시작한다. 큐에서 요소를 하나 꺼낸다. 꺼내진 요..

컴퓨터는 이진수를 사용한다. 비트 연산을 통해서 우리는 더 빠른 연산을 할 수 있다. 비트마스킹의 장점 1. 빠른 연산 - 비트마스킹 연산은 상수 시간에 연산된다. 2. 간결한 코드 - 비트마스킹을 통해 간결한 코드 표현이 가능하다. 3. 적은 메모리 사용 - 큰 크기의 숫자를 적은 메모리로 표현이 가능하다. 비트 연산들 and(&) 둘 다 참일 때에만 1 반환 ex) 1010 & 1111 = 1010 or(|) 둘 중 하나만 참일 때 1 반환 ex) 1000 | 1101 = 1101 xor(^) 둘이 서로 다를 때 1반환 ex) 1010 ^ 1111 = 0101 not(~) 반대 값을 반환 ex) ~1010 = 0101 시프트 연산() 비트 자릿수를 옮김. 001101

십진수를 이진수로 표기하고, 이진수 표기에서 1을 구하고 싶다면, 십진수 i를 2로 나눈 값 i/2의 1의 개수에, i가 홀수면 1을 더하고, 짝수인 경우 더하지 않으면 된다. #include // 십진수를 이진수로 변환하고 1의 개수를 구하는 함수 int countOnesInBinary(int n) { int count = 0; while (n > 0) { count += n % 2; // 현재 비트가 1이면 count에 1을 더함 n /= 2; // 십진수를 2로 나눔 } return count; } int main() { int i = 25; // 예시로 25를 사용 int binaryCount = countOnesInBinary(i); std::cout

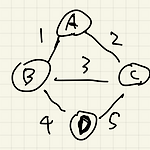
최소 신장 트리 (Minimum Spanning Tree, MST) 신장 트리는 그래프의 모든 정점을 연결하는 트리를 말한다. (사이클이 생기지 않음) 최소 신장 트리는 그래프의 모든 정점을 연결하는 간선들의 가중치의 합이 최소인 트리를 말한다. (신장 트리중 가장 저렴한 비용) 크루스칼 알고리즘(Kruscal's Algorithm) 크루스칼 알고리즘은 최소 신장 트리를 찾는 방법 중 하나이다. 1. 모든 간선들을 가중치 기준으로 오름차순 정렬한다. 2. 가장 작은 가중치의 간선부터 선택한다. 3. 고른 간선이 사이클을 형성한다면, 선택하지 않는다. 4. 2와3을 계속 반복한다. 아래는 크루스칼 알고리즘의 예시이다. 우선, 간선들의 가중치를 기준으로 오름차순 정렬해준다. A-B : 1 A-C : 2 B-..

투 포인터 말 그대로 두개의 포인터를 사용하는 알고리즘이다. (left, right), (start, end)처럼 주로 이름을 붙인다. 슬라이딩 윈도우 투 포인터와 비슷하나, 두 포인터간의 간격이 일정하다.

백트래킹 기법은 해를 찾는 도중, 해가 될 가능성이 없으면 이전으로 되돌아가면서 시간을 아끼는 방법이다. 보통 구현 방식은 DFS의 중간에 조건식을 넣어서, 더 깊게 들어가봤자 의미가 없다는 것을 판단시킨 후, 이전으로 돌아가게 하는 식으로 한다. 이 과정을 가지치기라고 하고, 이 가지치기의 조건을 얼마나 잘 설정하느냐가 관건이 된다.

Brute Force. 무식한 힘이란 뜻인데, 풀어 말하면 무식하게 풀기라고 할 수 있다. 완전히 모든 경우를 탐색하여 조건에 맞는 결과를 가져오는 것이다. 속도가 어떻게 될지라도, 반드시 결과를 가져온다. 선형 구조에서는 주로 순차 탐색, 비선형 구조에서는 BFS와 DFS등을 주로 사용한다. 장점으로는 반드시 답을 찾는다는 점이고, 단점으로는 느리거나 메모리를 많이 사용할 수 있다는 점이다. 브루트 포스의 문제 해결 과정 1. 주어진 문제를 구조화 한다. 2. 구조화 된 문제의 모든 해를 구하도록 탐색한다. 3. 구성된 해를 정리한다.

"당장 최선의 수를 고려하기" 탐욕 알고리즘은 매 선택마다 당장의 최선의 선택을 하여 답에 도달하는 방법이다. 항상 최선의 결과를 보여주지는 않지만 특정 상황들 속에서는 굉장히 효과적이고, 직관적이다. 대표적인 예시로는, 거스름돈이 있다. #include #include using namespace std; int input; int wons[4] = {500, 100, 50, 10}; vector calc_coin(int money) { vector coins = vector(4); coins[0] = money / 500; coins[1] = (money % 500) / 100; coins[2] = (money % 100) / 50; coins[3] = (money % 50) / 10; return ..