넘치게 채우기
[LeetCode] 947. Most Stones Removed with Same Row or Column 본문
[LeetCode] 947. Most Stones Removed with Same Row or Column
riveroverflow 2024. 8. 29. 12:33leetcode - Most Stones Removed with Same Row or Column
문제 유형 : 유니온-파인드
문제 난이도 : Medium
문제
On a 2D plane, we place n stones at some integer coordinate points. Each coordinate point may have at most one stone.
A stone can be removed if it shares either the same row or the same column as another stone that has not been removed.
Given an array stones of length n where stones[i] = [xi, yi] represents the location of the ith stone, return the largest possible number of stones that can be removed.
2D판에서, 우리는 n개의 돌을 각 정수에 상응하는 점에 놓는다.
각 점은 최대 하나의 돌이 있다.
만약 돌이 같은 행 또는 같은 열을 공유하는 다른 돌과 있다면, 그 돌은 제거될 수 있다.
stones[i] = [xi, yi]인 2D배열 stones가 주어진다.
최대로 가져갈 수 있는 돌의 개수를 구하시오.
풀이
유니온-파인드로 해결할 수 있다.
어떻게 유니온-파인드로 하느냐?
우선, row와 col을 구분해서 식별해주어야 한다.
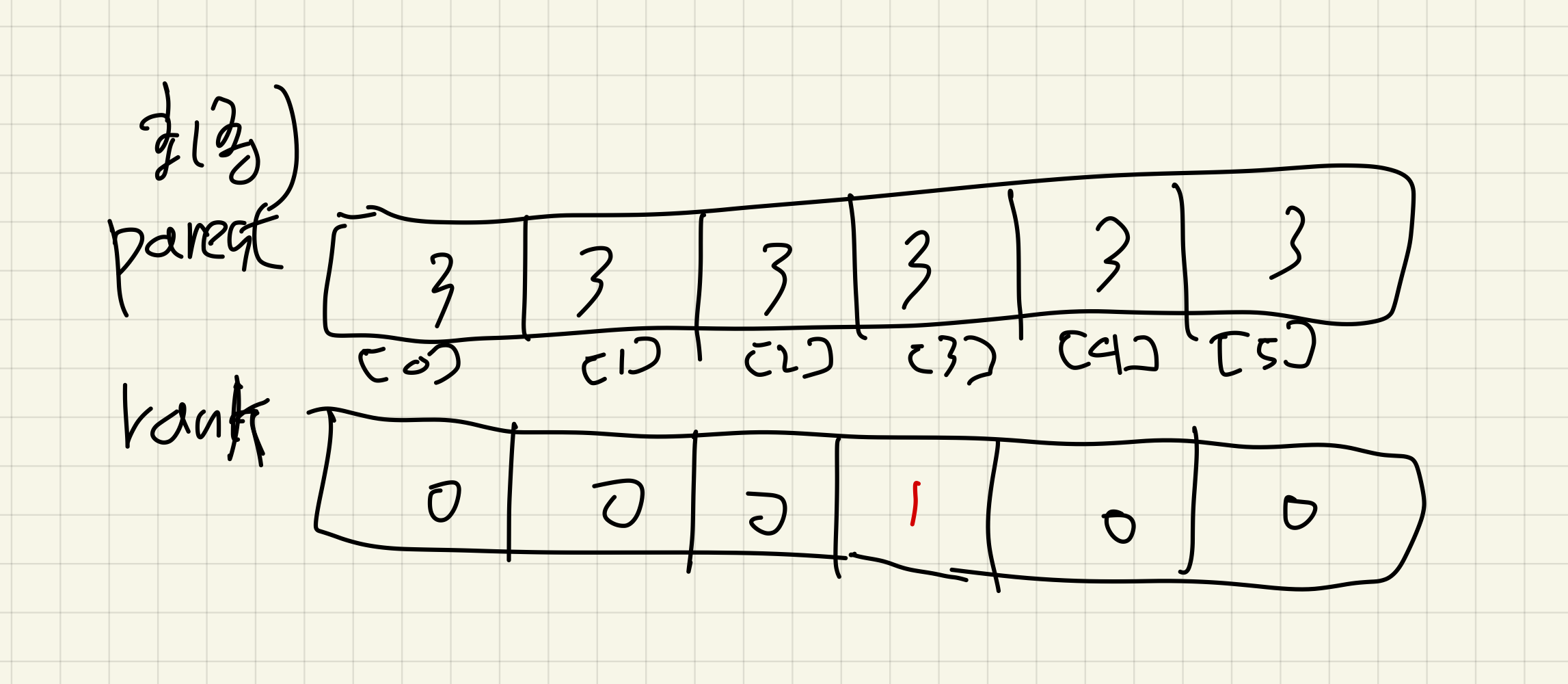
그렇게 하기 위해, col에는 maxRow만큼의 오프셋을 지정해서 식별 번호를 만든다.
그리고, 두 식별번호 row, col을 union-find시켜서, 한 소속으로 묶는다.
각각의 row, col을 묶으면, 결국 같은 행과 열을 공유하는 노드들끼리 체인이 맺어진다.
중간에 빈 숫자들은 의미 없는 값으로, 최종 정산에서 혼란을 줄 수 있으므로, 등장한 수들을 따로 마킹해놓는다.
이를 계속한다.
최종적으로, 등장했던 노드 식별자들에 대해 각자의 root찾아서 만약 자기 자신의 식별자와 같다면, 카운트를 센다
그렇게 센 카운트는 총 그룹의 개수이다.
모든 돌의 개수 - 총 그룹 수를 뺴면, 각 그룹에서 루트를 제외하고 돌을 주웠다고 가정했을 때의 수가 된다.

코드
C++
class Union {
public:
vector<int> rank, parent;
Union(int n) {
rank.resize(n+1, 1);
parent.resize(n+1);
for(int i = 0; i <= n; i++) {
parent[i] = i;
}
}
int find(int x) {
if(x == parent[x]) return x;
return parent[x] = find(parent[x]);
}
void unionSet(int u, int v) {
int uRoot = find(u);
int vRoot = find(v);
if(uRoot == vRoot) return;
if(rank[uRoot] < rank[vRoot]) {
parent[uRoot] = vRoot;
rank[vRoot] += rank[uRoot];
} else {
parent[vRoot] = uRoot;
if(rank[uRoot] == rank[vRoot]) {
rank[vRoot]++;
}
}
}
};
class Solution {
public:
int removeStones(vector<vector<int>>& stones) {
int n = stones.size();
int rMax = 0;
int cMax = 0;
for(const auto &stone : stones) {
rMax = max(rMax, stone[0]);
cMax = max(cMax, stone[1]);
}
Union u(rMax+cMax+1);
unordered_map<int, int> mp;
for(auto &stone : stones) {
int row = stone[0];
int col = stone[1] + rMax + 1;
u.unionSet(row, col);
mp[row] = 1;
mp[col] = 1;
}
int cnt = 0;
for(const auto &element : mp) {
if(u.find(element.first) == element.first) cnt++;
}
return n-cnt;
}
};
GO
type union struct {
rank []int
parent []int
}
func (u *union) find(x int) int {
if u.parent[x] != x {
u.parent[x] = u.find(u.parent[x])
}
return u.parent[x]
}
func (u *union) unionSets(x, y int) {
rootX := u.find(x)
rootY := u.find(y)
if rootX != rootY {
if u.rank[rootX] > u.rank[rootY] {
u.parent[rootY] = rootX
u.rank[rootX] += u.rank[rootY]
} else {
u.parent[rootX] = rootY
if u.rank[rootX] == u.rank[rootY] {
u.rank[rootY]++
}
}
}
}
func removeStones(stones [][]int) int {
n := len(stones)
maxRow, maxCol := 0, 0
for _, stone := range stones {
if stone[0] > maxRow {
maxRow = stone[0]
}
if stone[1] > maxCol {
maxCol = stone[1]
}
}
u := union{
rank: make([]int, maxRow+maxCol+2),
parent: make([]int, maxRow+maxCol+2),
}
for i := 0; i <= maxRow+maxCol+1; i++ {
u.parent[i] = i
}
for _, stone := range stones {
row := stone[0]
col := stone[1] + maxRow + 1
u.unionSets(row, col)
}
uniqueParents := make(map[int]struct{})
for _, stone := range stones {
root := u.find(stone[0])
uniqueParents[root] = struct{}{}
}
return n - len(uniqueParents)
}'PS > LeetCode' 카테고리의 다른 글
| [LeetCode] 2022. Convert 1D Array Into 2D Array (0) | 2024.09.01 |
|---|---|
| [LeetCode] 2699. Modify Graph Edge Weights (0) | 2024.08.30 |
| [LeetCode] 1905. Count Sub Islands (0) | 2024.08.28 |
| [LeetCode] 1514. Path with Maximum Probability (0) | 2024.08.27 |
| [LeetCode] 590. N-ary Tree Postorder Traversal (0) | 2024.08.26 |
