넘치게 채우기
[LeetCode] 2127. Maximum Employees to Be Invited to a Meeting 본문
[LeetCode] 2127. Maximum Employees to Be Invited to a Meeting
riveroverflow 2025. 1. 26. 18:15https://leetcode.com/problems/maximum-employees-to-be-invited-to-a-meeting/description/
leetcode -Maximum Employees to Be Invited to a Meeting
문제 유형: 위상 정렬, bfs, 연결 컴포넌트, 그래프
문제 난이도: Hard
문제
A company is organizing a meeting and has a list of n employees, waiting to be invited. They have arranged for a large circular table, capable of seating any number of employees.
The employees are numbered from 0 to n - 1. Each employee has a favorite person and they will attend the meeting only if they can sit next to their favorite person at the table. The favorite person of an employee is not themself.
Given a 0-indexed integer array favorite, where favorite[i] denotes the favorite person of the ith employee, return the maximum number of employees that can be invited to the meeting.
회사에서 n명의 리스트를 가지고 있다. 미팅을 하려고 하는데, 원형 테이블이 하나 있다.
몇 명이고 수용가능하다.
사원번호는 0부터 n-1번까지 있다.
각 사원은 가장 좋아하는 사원이 있는데, 그 사원이 참석해서 바로 옆에 앉는다는 전제하에 회의에 참여한다.
최대 참여자 수를 구하시오.
풀이
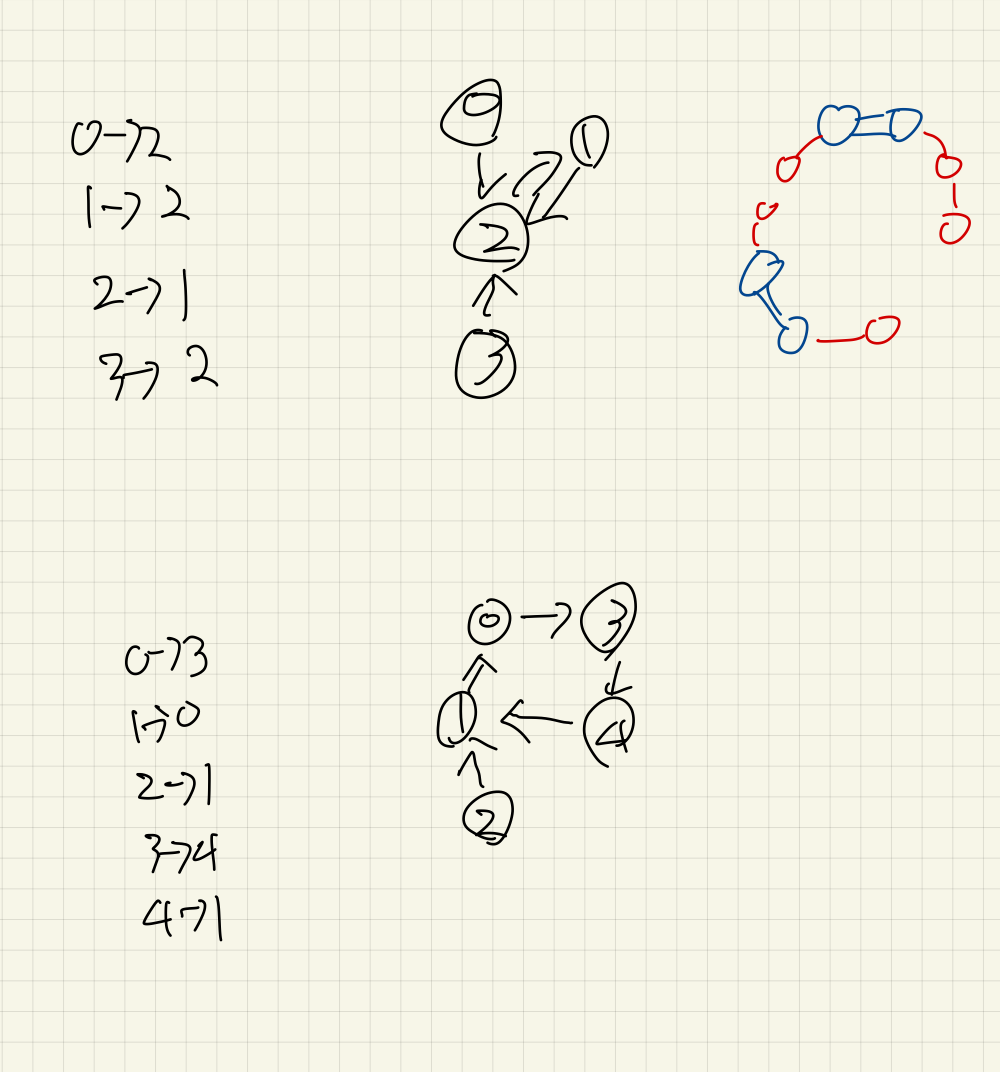
그림을 보면 알 수 있듯이, 사이클이 중점이다.
크기가 2인 사이클에는 각자 한명씩 그 사람을 좋아하는 사람과 또 그 사람을 좋아하는 사람의 체인을 데려올 수 있다.
크기가 3 이상인 사이클은 그 사이클로만 참여해야 한다.
즉, max((크기가 2인 사이클들의 개수 * 2 + 각 사이클의 노드에 연결된 DAG의 크기들), (크기가 3 이상인 사이클 들 중에서 가장 큰 사이클))이다.
우선 위상정렬을 먼저 해서, 각 DAG들이 어디에 의존하는지 구한다.
위상정렬하면서 방문하지 않은 곳들은 모두 사이클인데, 사이클이 2인 경우, 2 + 두 노드에 각각 의존하는 DAG의 최대크기를 가져온다.
3이상의 사이클은 따로 담아놓는다.
최종 답을 구한다.
코드
C++
class Solution {
public:
int maximumInvitations(vector<int>& favorite) {
int n = favorite.size();
vector<int> indegree(n, 0);
vector<bool> visited(n, false);
vector<int> maxDAG(n, 0);
for(int i = 0; i < n; ++i) {
indegree[favorite[i]]++;
}
queue<int> q;
for(int i = 0; i < n; ++i) {
if(indegree[i] == 0) q.push(i);
}
while(!q.empty()) {
int curr = q.front();
q.pop();
visited[curr] = true;
maxDAG[favorite[curr]] = max(maxDAG[favorite[curr]], maxDAG[curr]+1);
indegree[favorite[curr]]--;
if(indegree[favorite[curr]] == 0) q.push(favorite[curr]);
}
int over2Cycles = 0;
vector<int> over3Cycles;
for(int i = 0; i < n; ++i) {
if(!visited[i]) {
visited[i] = true;
int next = favorite[i];
vector<int> members = {i};
while(!visited[next]) {
visited[next] = true;
members.emplace_back(next);
next = favorite[next];
}
if(members.size() == 2) {
int dagA = maxDAG[members[0]];
int dagB = maxDAG[members[1]];
over2Cycles += 2 + dagA + dagB;
} else {
over3Cycles.emplace_back(members.size());
}
}
}
int b = over3Cycles.empty() ? 0 : *max_element(over3Cycles.begin(), over3Cycles.end());
int ans = max(over2Cycles, b);
return ans;
}
};
// over 3-sized cycle vs sum of 2-sized cycles + other DAGs
// 0. DAG-like components 구하기
// 1. cycle들 구해서 2-sized와 over 3-sized들 구하기
// 개수(DAG-like들 + 2-sized) vs 3-sized cycles들중 최대개수'PS > LeetCode' 카테고리의 다른 글
| [LeetCode] 658. Maximum Number of Fish in a Grid (0) | 2025.01.28 |
|---|---|
| [LeetCode] 1462. Course Schedule IV (0) | 2025.01.27 |
| [LeetCode] 2948. Make Lexicographically Smallest Array by Swapping Elements (0) | 2025.01.25 |
| [LeetCode] 802. Find Eventual Safe States (0) | 2025.01.24 |
| [LeetCode] 1267. Count Servers that Communicate (0) | 2025.01.23 |

