넘치게 채우기
[BOJ] 1799 - 비숍 본문
https://www.acmicpc.net/problem/1799
BOJ - 비숍
문제 유형: 백트래킹, 브루트 포스, MITM(Meet-In-The-Middle)
문제 난이도: Platinum V
시간 제한: 10초
메모리 제한: 128MB
문제
서양 장기인 체스에는 대각선 방향으로 움직일 수 있는 비숍(bishop)이 있다. < 그림 1 >과 같은 정사각형 체스판 위에 B라고 표시된 곳에 비숍이 있을 때 비숍은 대각선 방향으로 움직여 O로 표시된 칸에 있는 다른 말을 잡을 수 있다.

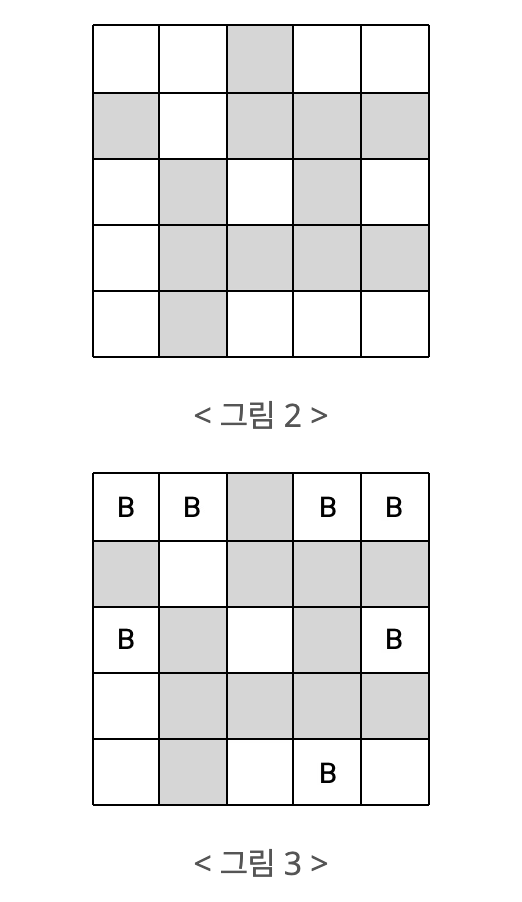
그런데 체스판 위에는 비숍이 놓일 수 없는 곳이 있다. < 그림 2 >에서 체스판에 색칠된 부분은 비숍이 놓일 수 없다고 하자. 이와 같은 체스판에 서로가 서로를 잡을 수 없도록 하면서 비숍을 놓는다면 < 그림 3 >과 같이 최대 7개의 비숍을 놓을 수 있다. 색칠된 부분에는 비숍이 놓일 수 없지만 지나갈 수는 있다.
정사각형 체스판의 한 변에 놓인 칸의 개수를 체스판의 크기라고 한다. 체스판의 크기와 체스판 각 칸에 비숍을 놓을 수 있는지 없는지에 대한 정보가 주어질 때, 서로가 서로를 잡을 수 없는 위치에 놓을 수 있는 비숍의 최대 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 체스판의 크기가 주어진다. 체스판의 크기는 10이하의 자연수이다. 둘째 줄부터 아래의 예와 같이 체스판의 각 칸에 비숍을 놓을 수 있는지 없는지에 대한 정보가 체스판 한 줄 단위로 한 줄씩 주어진다. 비숍을 놓을 수 있는 곳에는 1, 비숍을 놓을 수 없는 곳에는 0이 빈칸을 사이에 두고 주어진다.
출력
첫째 줄에 주어진 체스판 위에 놓을 수 있는 비숍의 최대 개수를 출력한다.
풀이
처음에는 마킹 최적화까지는 생각했었는데 두 개의 보드로 분할할 생각을 못 했었다...
단순한 백트래킹으로는 TLE에 걸린다.
우리는 밝은 색 비숍과 어두운 색 비숍이 서로 관계없다는걸 알 수 있다.
즉, 밝은 색 따로, 어두운 색 따로 백트래킹을 돌리면, 훨씬 최적화된 풀이가 가능하다.
그리고 밝은색의 최대개수와 어두운 색의 최대개수를 더해서 출력하면 되는 것이다.
또한, 그 대각선이 사용중인지에 대한 마킹을 하는 것도 최적화가 필요하다.
우상향 대각선이 있고, 우하향 대각선이 있다.
(r, c)에서 현재 소속된 대각선의 id를 다음과 같이 구해주었다:
우상향 대각선: r+c번. 즉, 둘의 합이다.
좌상향 대각선: r-c+offset(9)번. 즉, 둘의 차에다가 음수방지를 위해 오프셋을 더해준 값이다.
각 방향별로 대각선은 19개씩 있음을 알 수 있다.

색깔별로 백트래킹을 하므로, 다음 칸으로 넘어갈 때, (r, c)에서 c+2로 이동해야 한다.
단, c+2가 n 이상이면, 다음 줄로 넘어가야 하는데, 홀수인 경우 단지 n을 빼주기만 하면 되지만,
짝수인 경우에는 이렇게만 했다가는 쭉 같은 열로 탐색하게 되는데, 이러면 어긋나게 된다.
대신, n을 빼고난 뒤 0 또는 1일 것인데, 1과 xor하여 비트플립을 시켜주면 된다.
백트래킹의 구현은 간단하다. 현재 칸이 설치가능하다면, 즉 보드 값이 1이고 현재 소속된 대각선이 비어있음이 확인된다면, 대각선을 채워주고 재귀호출 후 원상복구하면 비숍을 설치한 것을 가정하고 호출한 것이다.
그 뒤, 설치가능하던 불가능하던 다음 칸으로 넘기면 된다.
최종적으로, 밝은색의 최대개수와 어두운색의 최대개수를 합한게 정답이다.
코드
C++
#include <bits/stdc++.h>
using namespace std;
int n;
int ans[2]; // code0 - 밝은색, code1 - 어두운색
const int offset = 9;
int board[10][10]; // 0: wall 1: available
bool diagD[19]; // 우하향 대각선
bool diagU[19]; // 우상향 대각선
void solve(int r, int c, int code, int count) {
if (r >= n) {
ans[code] = max(ans[code], count);
return;
}
int diagD_id = r - c + offset;
int diagU_id = r + c;
// 가능한경우 백트래킹
if (board[r][c] == 1 && !diagD[diagD_id] && !diagU[diagU_id]) {
diagD[diagD_id] = true;
diagU[diagU_id] = true;
board[r][c] = 2;
if (c + 2 >= n) {
int newC = c + 2 - n;
if (n % 2 == 0)
newC ^= 1;
solve(r + 1, newC, code, count + 1);
} else
solve(r, c + 2, code, count + 1);
diagD[diagD_id] = false;
diagU[diagU_id] = false;
board[r][c] = 1;
}
// 그냥 보내기
if (c + 2 >= n) {
int newC = c + 2 - n;
if (n % 2 == 0)
newC ^= 1;
solve(r + 1, newC, code, count);
} else
solve(r, c + 2, code, count);
}
int main(int argc, char *argv[]) {
cin >> n;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
cin >> board[i][j];
}
}
solve(0, 0, 0, 0);
solve(0, 1, 1, 0);
cout << ans[0] + ans[1] << "\n";
return 0;
}'PS > BOJ' 카테고리의 다른 글
| [BOJ] 10775 - 공항 (0) | 2025.01.24 |
|---|---|
| [BOJ] 28707 - 배열 정렬 (0) | 2025.01.23 |
| [BOJ] 1509 - 팰린드롬 분할 (0) | 2025.01.21 |
| [BOJ] 4963 - 섬의 개수 (0) | 2025.01.20 |
| [BOJ] 2468 - 안전 영역 (0) | 2025.01.20 |


