넘치게 채우기
2-4. 함수형 프로그래밍 본문
여러 가지 의미로, 함수형 프로그래밍이라는 개념은 프로그래밍 그 자체보다 앞섰다.
이 패러다임에서 핵심이 되는 기반은 람다(lambda)계산법으로, 알론조 처지(Alonzo Church)가 1930년대에 발명했다.
정수를 제곱하기
25까지의 정수의 제곱을 출력하는 간단한 문제를 다뤄보자.
자바 언어라면 아래처럼 작성할 수 있다.
public class Squint {
public static void main(String args[]) {
for(int i = 0; i < 25; i++) {
System.out.println(i*i);
}
}리스프에서 파생한 클로저(Clojure)는 함수형 언어로, 클로저를 이용하면 같은 프로그램을 다음과 같이 구현한다.
(println (take 25(map (fn [x] (* x x)) (range))))위의 코드가 생소할 수 있다.
다음과 같이 작성하고 주석을 달아보자.
(println ;___ 출력한다.
(take 25 ;___ 처음부터 25까지
(map (fn[x] (* x x)) ;__ 제곱을
(range)))) ;___정수의println, take, map, range는 모두 함수다. 리스프에서는 함수를 괄호 안에 넣는 방식으로 호출한다.
예를 들어 (range)는 range 함수를 호출한다.
표현식 (fn [x] (* x x))는 익명 함수(anonymous function)로, 곱셈 함수를 호출하면서 입력 인자를 두 번 전달한다. 즉 입력의 제곱을 계산한다.
전체 코드를 다시 봐보자. 가장 안쪽의 함수 호출부터 시작하는게 가장 좋다.
range함수는 0부터 시작해서 끝이 없는 정수 리스트를 반환한다.- 반환된 정수 리스트는
map함수로 전달되고, 각 정수에 대해 제곱을 계산하는 익명 함수를 호출하여, 모든 정수의 제곱에 대해 끝이 없는 리스트를 생성한다. - 제곱된 리스트는
take함수로 전달되고, 이 함수는 앞의 25개까지의 항목으로 구성된 새로운 리스트를 반환한다. println함수는 입력 값을 출력하는데, 이 경우 입력은 앞의 25개의 정수에 대한 제곱 값으로 구성된 리스트다.
끝이 없는 리스트라는 개념에 놀랄 수도 있지만, 실제로는 끝이 없는 리스트 중에서 앞의 25개까지만 생성될 뿐이다. 끝이 없는 리스트의 어떤 항목도 실제로 접근하기 전에는 평가기 이뤄지지 않기 때문이다.
자바 프로그램은 가변 변수(mutable variable)을 사용하는데, 가변 변수는 프로그램 실행 중에 상태가 변할 수 있다. 앞의 예제에서 반복문을 제어하는 변수가 i가 가변 변수다.
클로저 프로그램에는 이러한 가변 변수가 전혀 없다.
함수형 언어에서 변수는 변경되지 않는다.
불변성과 아키텍처
아키텍처를 고려할 때 이러한 내용이 왜 중요할까?
아키텍트는 왜 변수의 가변성을 염려하는가?
경합 조건, 교착상태 조건, 동시 업데이트 문제가 모두 가변 변수로 인해 발생하기 때문이다.
만약 어떠한 변수도 갱신되지 않는다면 경합 조건이나 동시 업데이트 문제가 일어나지 않는다. 락(lock)이 가변적이지 않다면 교착상태도 일어나지 않는다.
다시 말해 우리가 동시성 애플리케이션에서 마주치는 모든 문제, 즉 다수의 스레드와 프로세스를 사용하는 애플리케이션에서 마주치는 모든 문제는 가변 변수가 없다면 절대로 생기지 않는다.
아키텍트라면 동시성(cocurrency) 문제에 지대한 관심을 가져야만 한다.
우리는 스레드와 프로세스가 여러 개인 상황에서도 설계한 시스템이 여전히 강건하기를 바란다. 그렇다면 이제 불변성이 정말 실현 가능한지를 스스로에게 반드시 물어봐야 한다.
이 질문에 대한 대답은 긍정적이다. 저장 공간이 무한하고, 프로세서의 속도가 무한히 빠르다는 전제 하에 말이다.
불변성은 실현 가능하겠지만, 일종의 타협을 해야 한다.
가변성의 분리
불변성과 관련하여 가장 주요한 타협 중 하나는 애플리케이션, 또는 애플리케이션 내부의 서비스를 가변 컴포넌트와 불변 컴포넌트로 분리하는 일이다.
불변 컴포넌트에서는 순수하게 함수형 방식으로만 작업이 처리되며, 어떤 가변 변수도 사용되지 않는다. 불변 컴포넌트는 변수의 상태를 변경할 수 있는, 즉 순수 함수형 컴포넌트가 아닌 하나 이상의 다른 컴포넌트와 서로 통신한다.
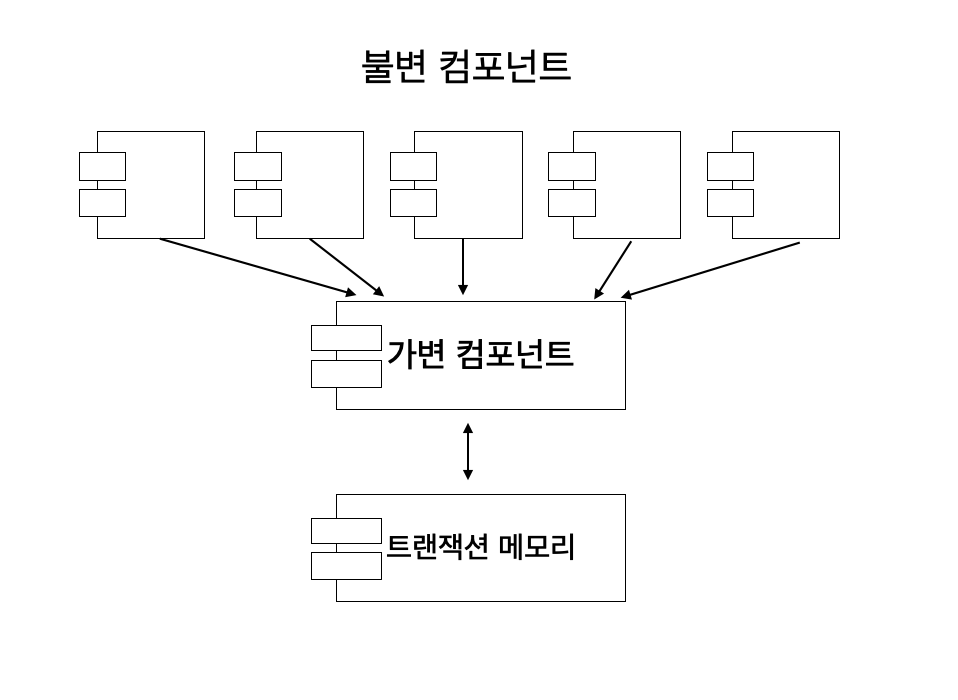
상태 변경은 컴포넌트를 갖가지 동시성 문제에 노출하는 꼴이므로, 흔히 트랜잭션 메모리와 같은 실천법을 사용하여 동시 업데이트와 경합 조건 문제로부터 가변 변수를 보호한다.
트랜젝션 메모리는 데이터베이스가 디스크의 레코드를 다루는 방식과 동일한 방식으로 메모리의 변수를 처리한다.
즉, 트랜잭션을 사용하거나 또는 재시도 기법을 통해 이들 변수를 보호한다.
애플리케이션을 제대로 구조화하려면, 변수를 변경하는 컴포넌트와 변경하지 않는 컴포넌트를 분리해야 한다는 것이다.
그리고 이렇게 분리하려면 가변 변수들을 보호하는 적절한 수단을 동원해 뒷받침해야 한다.
현명한 아키텍트라면 가능한 한 많은 처리를 불변 컴포넌트로 옮겨야 하고, 가변 컴포넌트에서는 가능한 한 많은 코드를 빼내야 한다.
이벤트 소싱
저장 공간과 처리 능력의 한계는 우리의 시야에서 급격히 사라지고 있다.
이제 프로세서가 초당 수십억 개의 명령을 수행하고, 램 용량은 수십억 바이트인 시대가 되었다.
더 많은 메모리를 확보할수록, 기계가 더 빨라질수록, 필요한 가변 상태는 더 적어진다.
간단한 예로, 고객의 계좌 잔고를 관리하는 은행 애플리케이션을 생각해보자.
이 애플리케이션에는 입금 트랜잭션과 출금 트랜잭션이 실행되면 잔고를 변경해야 한다.
이제 계좌 잔고를 변경하는 대신, 트랜잭션 자체를 저장한다고 상상해보자.
누군가 잔고 조회를 요청할 때마다 계좌 개설 시점부터 발생한 모든 트랜잭션을 단순히 더한다.
이 전략에서는 가변 변수가 하나도 필요 없다.
당연하게도 이 전략은 터무늬없다. 시간이 지날수록 트랜잭션 수는 끝없이 증가하고, 잔고 계산에 필요한 컴퓨팅 자원은 걷잡을 수 없이 커진다.
따라서 이 전략이 영원히 실현 가능하려면 무한한 저장 공간과 무한한 처리 능력이 필요하다.
하지만, 영원히 동작하도록 할 필요가 없다. 애플리케이션의 수명주기 동안만 문제 없이 동작해주면 된다.
이벤트 소싱(event sourcing)에 깔려있는 기본 발상이 바로 이것이다.
이벤트 소싱은 상태가 아닌 트랜잭션을 저장하자는 전략이다.
상태가 필요해지면 단순히 상태의 시작점부터 모든 트랜잭션을 처리한다.
중요한 점은 데이터 저장소에서 삭제되거나 변경되는 것이 하나도 없다는 사실이다. 결과적으로 애플리케이션은 CRUD가 아니라 그저 CR만 수행한다.
또한 데이터 저장소에서 변경과 삭제가 전혀 발생하지 않으므로 동시 업데이트 문제 또한 일어나지 않는다.
저장 공간과 처리 능력이 충분하면 애플리케이션이 완전한 불변성을 갖도록 만들 수 있고, 따라서 완전한 함수형으로 만들 수 있다.
'개발 > Clean Architecture' 카테고리의 다른 글
| 3-2. OCP: 개방-폐쇄 원칙(Open-Closed Principle) (0) | 2023.11.09 |
|---|---|
| 3-1. SRP: 단일 책임 원칙(Single Responsibility Principle) (0) | 2023.11.09 |
| 2-3. 객체 지향 프로그래밍 (0) | 2023.11.06 |
| 2-2. 구조적 프로그래밍 (0) | 2023.11.05 |
| 2-1. 패러다임 개요 (0) | 2023.11.04 |



