넘치게 채우기
[알고리즘] 3. 정렬(Sort) 본문
정렬은 데이터들을 주어진 조건에 맞게 순차적으로 나열하는 것이다.
1. 버블 정렬(Bubble Sort)

한 번 순회할 때마다 마지막 하나가 정렬 된다.
거품이 올라오는 것 처럼 보여서 버블 정렬이라고 한다.
두 수를 비교하여, 조건에 맞으면 자리를 바꾼다.
O(N^2)의 시간복잡도를 가진다.
def bubble_sort(arr):
for i in range(len(arr)):
for j in range(len(arr)):
if arr[i] < arr[j]:
arr[i], arr[j] = arr[j], arr[i]
2. 선택 정렬(Selection Sort)

테이블에서 가장 작은 노드를 찾아서 맨 앞으로 위치를 바꾼다.
맨 앞에 놓인 노드 뒤부터 다시 똑같은 과정을 반복한다.(가장 작은 노드를 0번째 인덱스에 넣었으면, 1번째 인덱스부터 다시 반복한다.)
O(N^2)의 시작복잡도를 가진다.
def selection_sort(arr):
for i in range(len(arr)):
min_index = i
for j in range(i+1, len(arr)):
if arr[min_index] > arr[j]:
min_index = j
arr[i], arr[min_index] = arr[min_index], arr[i]
3. 삽입 정렬(Insertion sort)
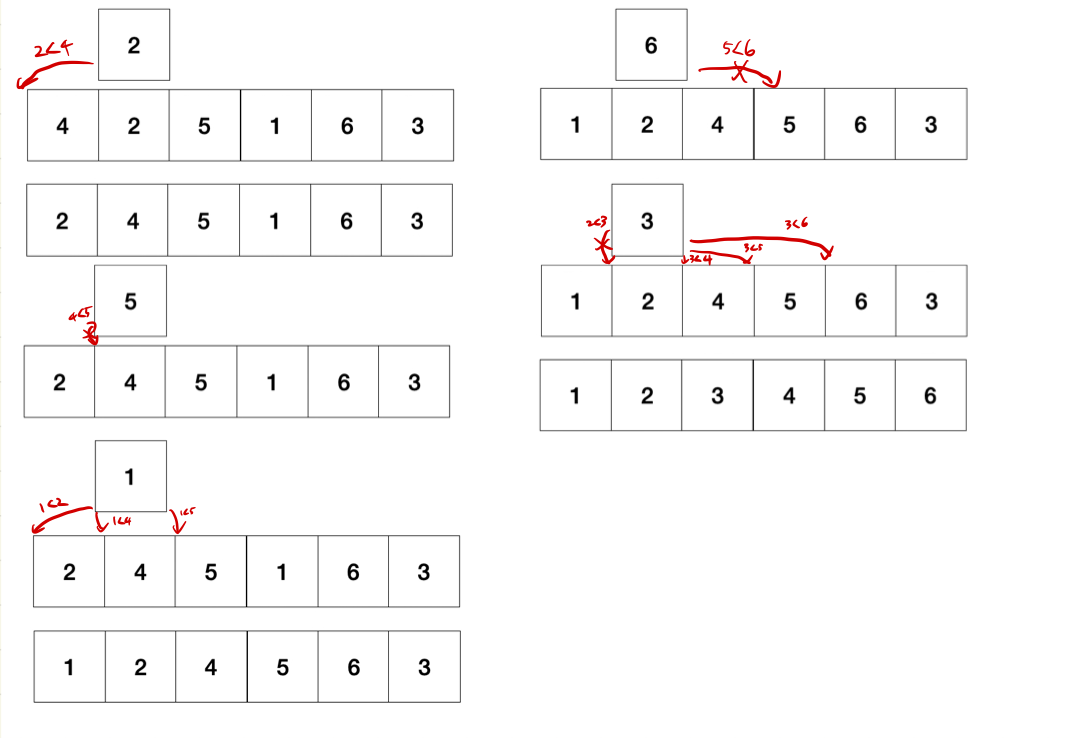
삽입 정렬은 사람이 카드를 들고 정렬하는 과정과 가장 유사하다.
데이터를 확인하여 적절한 위치에 삽입하는 정렬이다.
0번째 인덱스는 이미 정렬되어 있다고 가정한 뒤, 건너뛰고, 1번째 인덱스부터 들어서 0~1 중에서 어디에 넣을지를 정한다.
n번째 인덱스를 들 때에는 0~n중에서 위치를 고른다. 바로 뒤 인덱스부터 비교를 시작해서, 적절한 위치를 찾으면 뒤쪽 부분은 이미 정렬되어 있으므로 건너뛴다.
최선의 경우에서는 O(N), 최악의 경우에서는 O(N^2)의 시작복잡도를 가진다.
def insertion_sort(arr):
for i in range(1, len(arr)):
for j in range(i, 0, -1):
if arr[j] < arr[j-1]:
arr[j], arr[j-1] = arr[j-1], arr[j]
else:
break
4. 병합 정렬(Merge Sort)
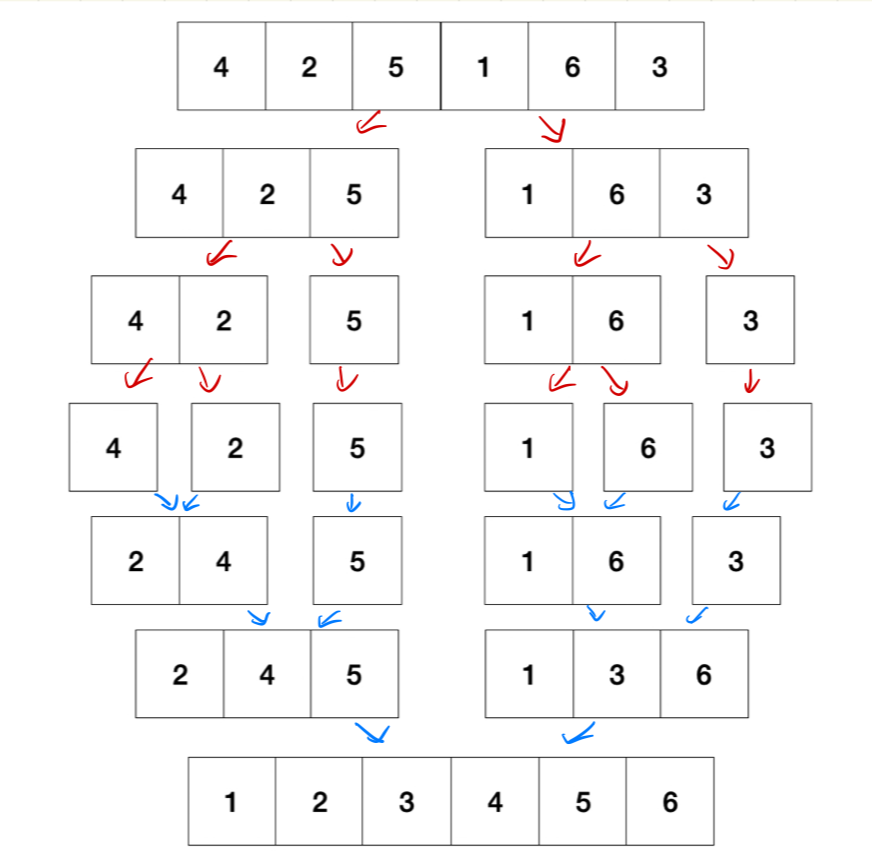
문제를 작은 문제로 쪼개서 해결하는 분할 정복법을 사용하고, 파이썬 기본 라이브러리의 sorted()함수에서 쓰이는 방법이다.
데이터를 다 쪼개고, 다시 합치는 과정에서 정렬한다.(재귀적으로 실행됨)
최악의 경우에도 O(NlogN)이 보장된다.
다시 합치는 과정에서, 양쪽에서 값을 비교하고, 더 작은 값을 먼저 배열에 넣고, 다시 비교하는 과정을 거친다.
def merge_sort(arr):
if len(arr) > 1:
mid = len(arr) // 2
left_arr = arr[:mid]
right_arr = arr[mid:]
merge_sort(left_arr)
merge_sort(right_arr)
i = j = k = 0
#양쪽에서 더 작은 값을 먼저 배열에 추가하는 과정
while i < len(left_arr) and j < len(right_arr):
if left_arr[i] < right_arr[j]:
arr[k] = left_arr[i]
i += 1
else:
arr[k] = right_arr[j]
j += 1
k += 1
while i < len(left_arr):
arr[k] = left_arr[i]
i += 1
k += 1
while j < len(right_arr):
arr[k] = right_arr[j]
j += 1
k += 1
return arr
5. 퀵 정렬(Quick Sort)

병합 정렬처럼, 분할 정복법을 사용한다.
한 요소를 고른다. 이를 피벗이라고 한다.
리스트를 '피벗보다 작은 수들', '피벗', '피벗보다 큰 수들'로 나눈다.
모든 요소들이 하나씩 분리될 때 까지 계속 위 과정을 반복한다.
모든 요소들이 분리되면, 분리된 요소들을 합쳐주면 된다.
분리가 되는 과정에서 순서가 정해졌으므로, 그래도 합치는 과정이 매우 간단하다.
평균적으로 O(NlogN)의 시간복잡도가 나온다.
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left_arr, right_arr, equal_arr = [], [], []
for i in arr:
if i > pivot:
right_arr.append(i)
elif i < pivot:
left_arr.append(i)
else:
equal_arr.append(i)
return quick_sort(left_arr) + equal_arr + quick_sort(right_arr)
6. 계수 정렬(Counting Sort)
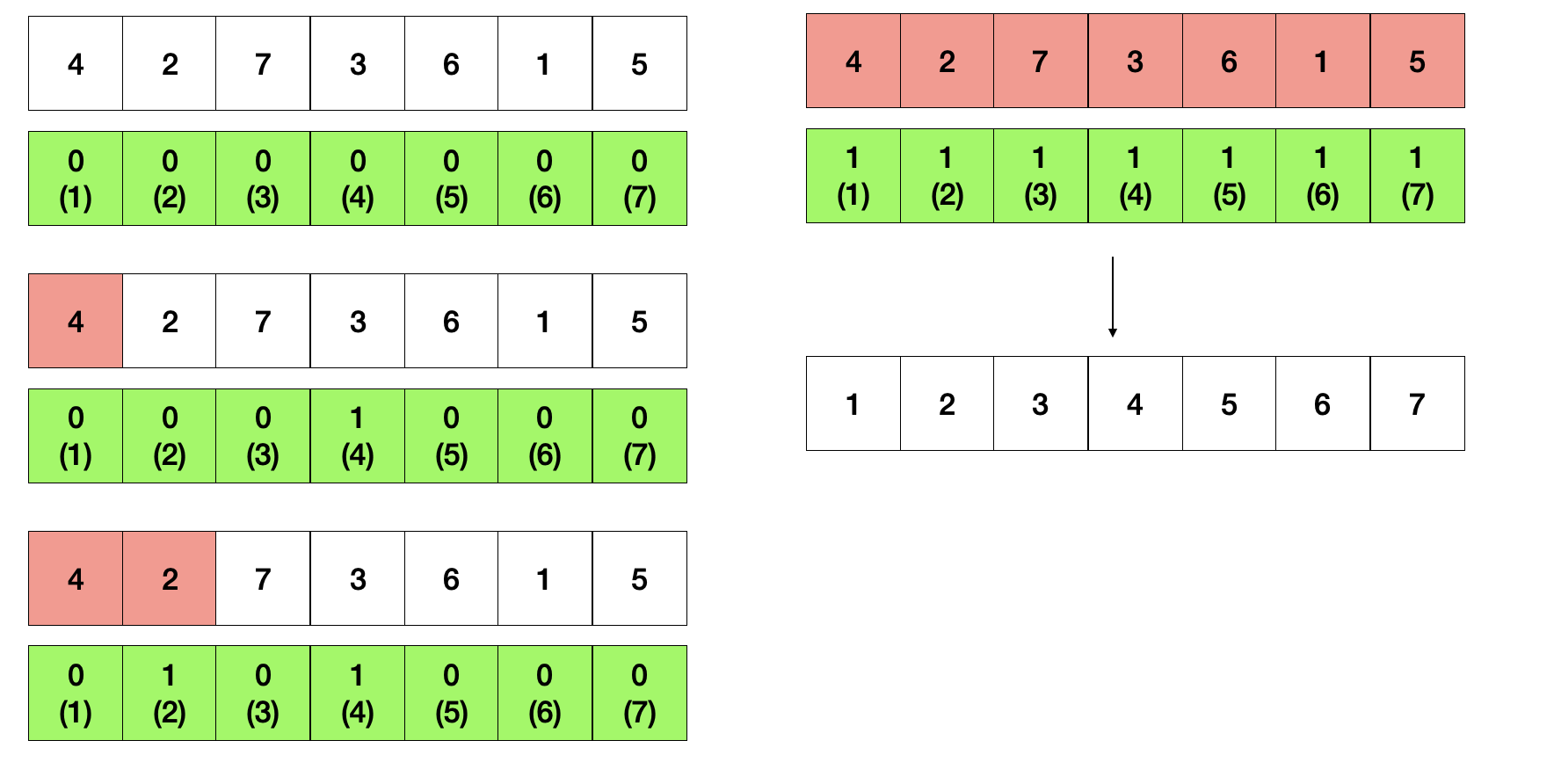
리스트를 데이터의 최대값인 K개만큼 만들고, 계수별로 개수를 측정해서 배열하는 방식이다.
위의 그림과 같이, 데이터의 범위가 작고, 중간에 비는 경우가 없는 때에 사용하기 좋다.
만약, [100, 1000, 1]의 배열을 정렬하는 경우에는, 1000칸짜리 배열을 만들어야 하므로 매우 비효율적이다.
시간복잡도는 O(N + K)가 걸린다. (K = 가장 큰 값)
def counting_sort(arr):
max_num = max(arr)
count = [0] * (max_num + 1)
for num in arr:
count[num] += 1
sorted_arr = []
for i in range(max_num + 1):
for j in range(count[i]):
sorted_arr.append(i)
return sorted_arr'컴퓨터과학 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 5. 탐욕법(Greedy) (0) | 2023.04.29 |
|---|---|
| [알고리즘] 4. 동적 계획법(Dynamic Programming) (0) | 2023.04.29 |
| [알고리즘] 2-2. 너비 우선 탐색(BFS) (0) | 2023.04.18 |
| [알고리즘] 2-1. 깊이 우선 탐색(DFS) (0) | 2023.04.18 |
| [알고리즘] 1. 재귀 함수(Recursion) (0) | 2023.04.17 |


