넘치게 채우기
[알고리즘] 최소 신장 트리와 크루스칼 알고리즘 본문
최소 신장 트리 (Minimum Spanning Tree, MST)
신장 트리는 그래프의 모든 정점을 연결하는 트리를 말한다. (사이클이 생기지 않음)
최소 신장 트리는 그래프의 모든 정점을 연결하는 간선들의 가중치의 합이 최소인 트리를 말한다. (신장 트리중 가장 저렴한 비용)
크루스칼 알고리즘(Kruscal's Algorithm)
크루스칼 알고리즘은 최소 신장 트리를 찾는 방법 중 하나이다.
1. 모든 간선들을 가중치 기준으로 오름차순 정렬한다.
2. 가장 작은 가중치의 간선부터 선택한다.
3. 고른 간선이 사이클을 형성한다면, 선택하지 않는다.
4. 2와3을 계속 반복한다.
아래는 크루스칼 알고리즘의 예시이다.
우선, 간선들의 가중치를 기준으로 오름차순 정렬해준다.
A-B : 1
A-C : 2
B-C : 3
B-D : 4
C-D : 5
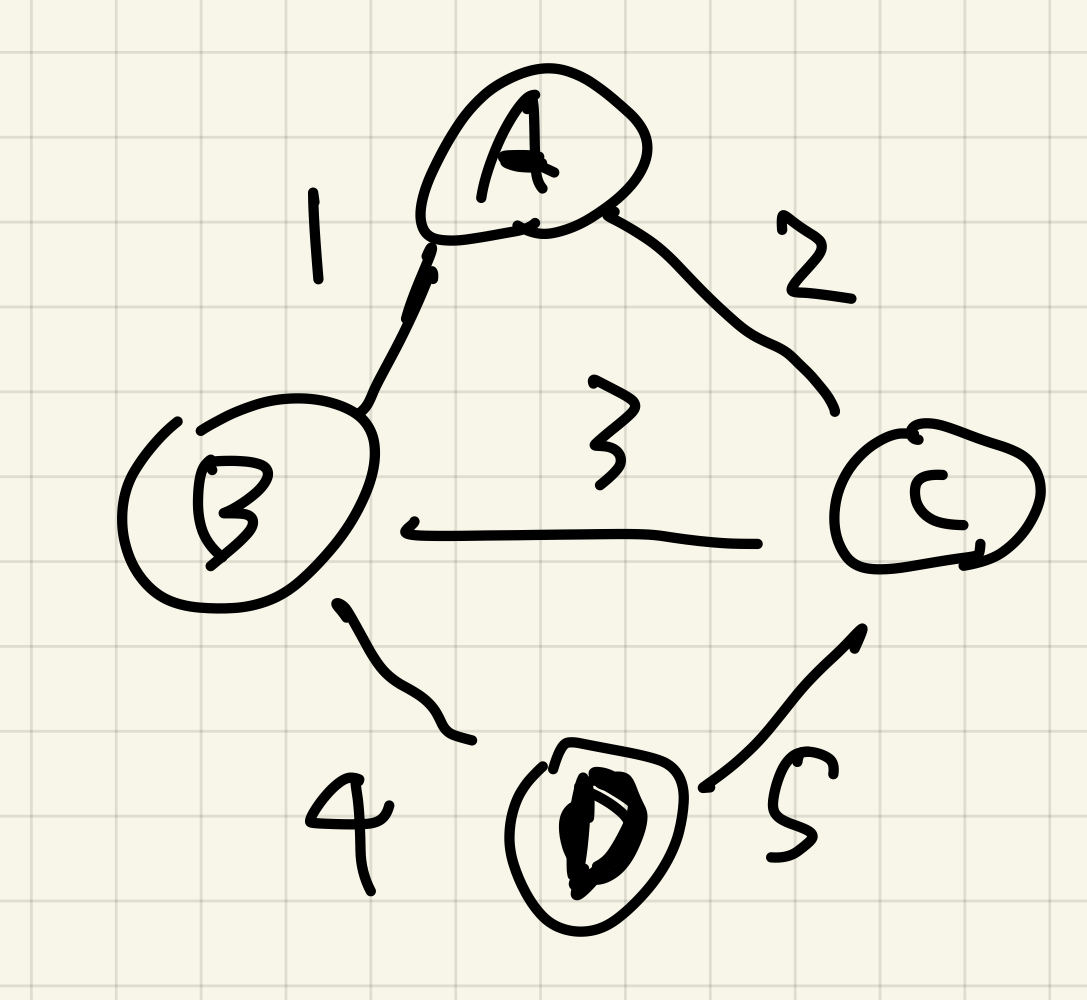
가장 비용이 낮은 간선 A-B부터 추가한다.
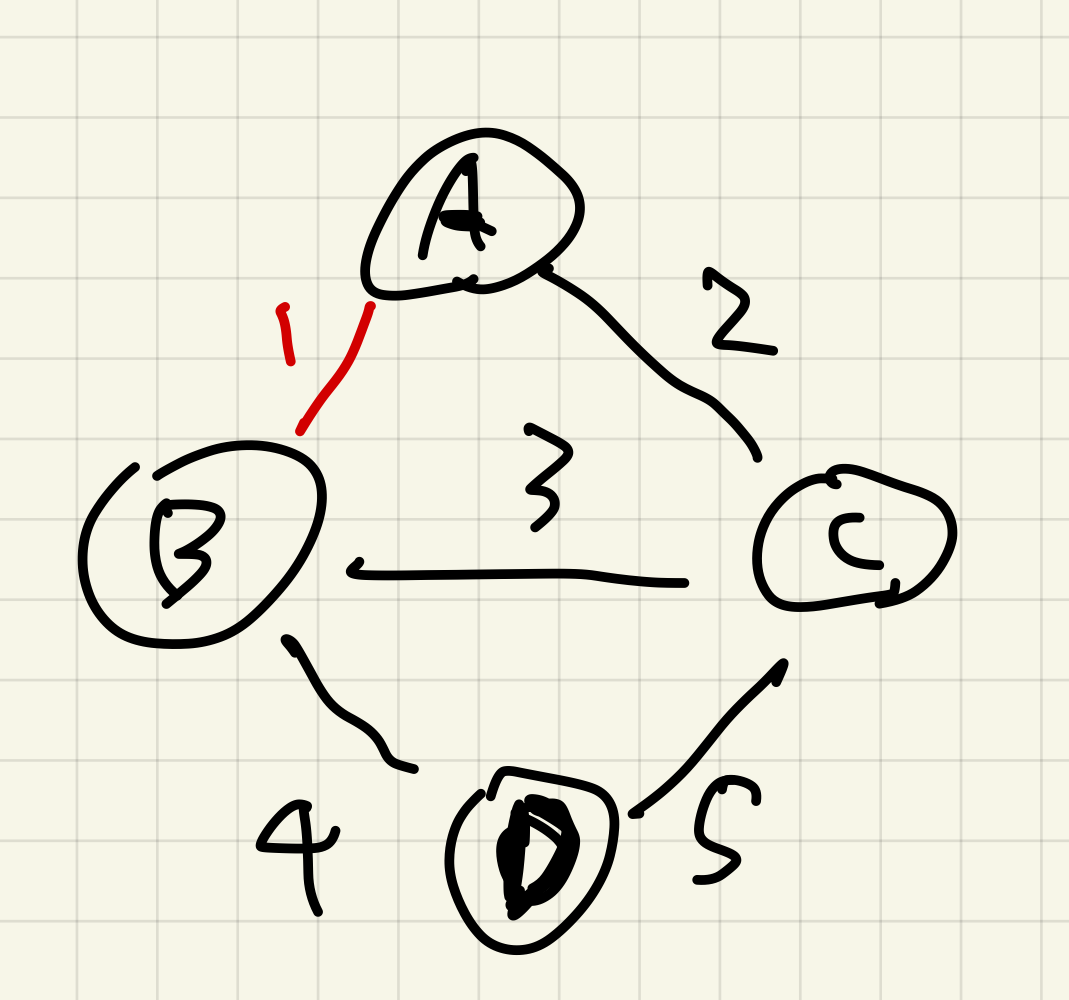
그 다음으로 비용이 낮은 A-C를 연결한다.

B-C가 그 다음으로 비용이 낮지만, 사이클이 생기므로 B-D를 연결한다. 최소 신장트리가 완성되고, 비용은 7이 된다.
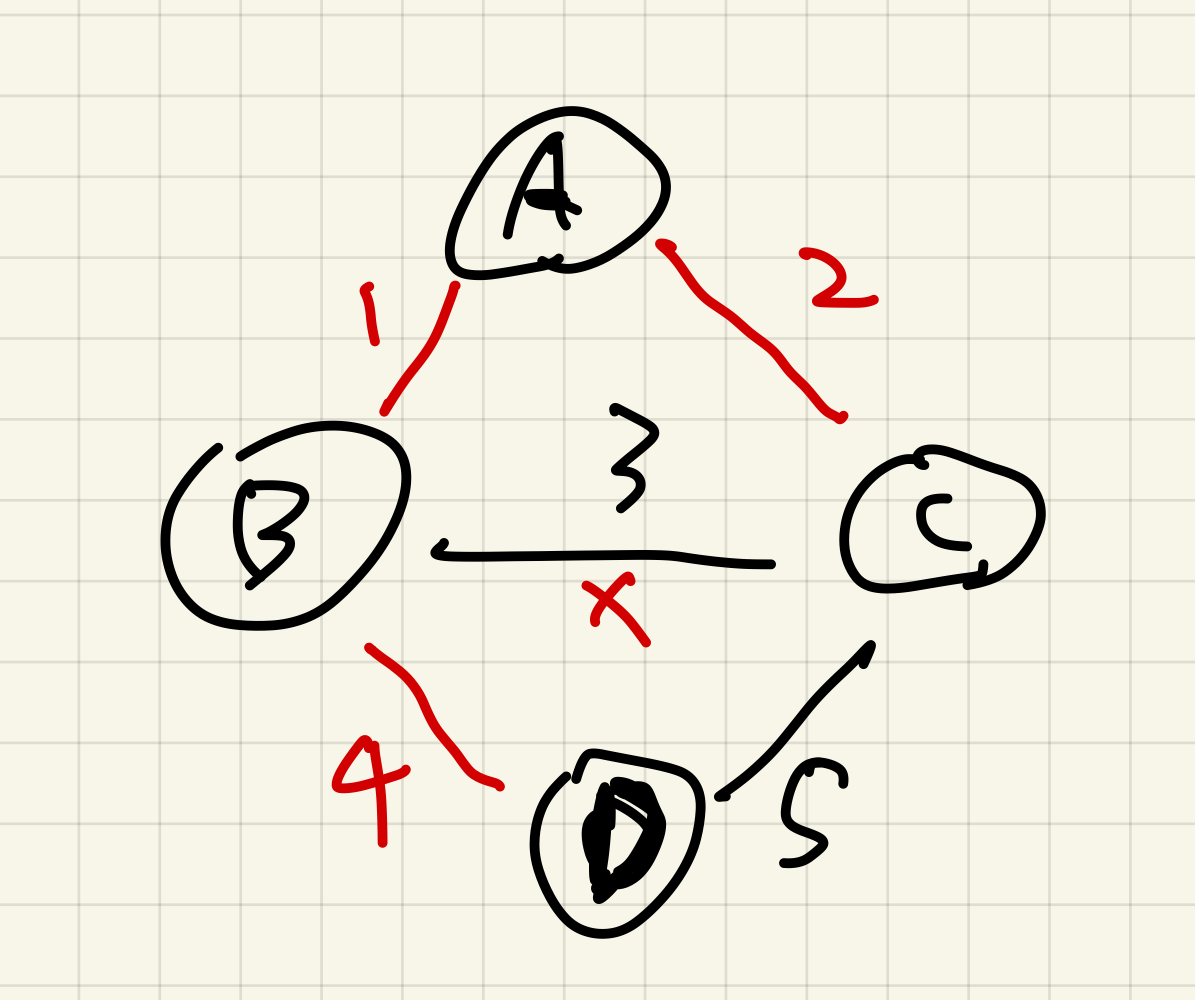
이 알고리즘은 간선의 개수 E에 대해서 O(E logE)의 시간복잡도를 가진다.
유니온-파인드
유니온-파인드 자료구조는 집합들의 합집합과 해당 원소가 어떤 집합에 포함되어 있는지를 찾을 수 있는 자료구조이다.
주로 크루스칼 알고리즘에서 사이클 검사를 위해 사용된다.
연산
1. FInd : 원소 x가 속한 집합의 대표(루트)를 반환한다.
2. Union : 두 집합을 합치는 연산을 한다.
동작 방식
초기화: 모든 원소가 각자의 집합에 속한 것으로 시작한다. 즉 각 원소는 자신이 대표자이다.
Find연산: 원소 x의 대표자를 찾기 위해 부모 노드를 따라가며 루트를 찾는다.
Union연산: 두 원소 x와 y의 대표자를 찾아, y의 대표자를 x의 대표자의 자식 노드로 만든다. 랭크를 사용하여 높이가 낮은 트리를 높은 트리에 붙이는 식으로 할 수 있다.
'컴퓨터과학 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 위상 정렬(Toplogiclal Sort) (0) | 2023.09.11 |
|---|---|
| 비트마스킹(bitmasking) (0) | 2023.09.11 |
| [알고리즘] 8. 투 포인터와 슬라이딩 윈도우 (Two Pointer && Sliding Window) (0) | 2023.05.07 |
| [알고리즘] 7. 백트래킹 기법(Backtracking) (0) | 2023.05.02 |
| [알고리즘] 6. 브루트 포스 기법(Brute Force) (0) | 2023.05.02 |

